Derive an expression for the variation of g with the height from the surface of Earth.
To derive the expression for the variation of acceleration due to gravity (g) with height (h) from the surface of the Earth, we can follow these steps:
1. Define the Variables:
- Let g be the acceleration due to gravity at the surface of the Earth.
- Let g′ be the acceleration due to gravity at a height h above the surface.
- Let R be the radius of the Earth.
2. Expression for g at the Surface:
- The acceleration due to gravity at the surface of the Earth is given by:
g=GMR2
where G is the universal gravitational constant and M is the mass of the Earth.
3. Expression for g' at Height h:
- At a height h above the surface, the distance from the center of the Earth becomes R+h. Therefore, the expression for g′ at this height is:
g′=GM(R+h)2
4. Relating g' to g:
- To find the relationship between g′ and g, we can take the ratio:
g′g=GM(R+h)2GMR2=R2(R+h)2
- The GM cancels out in the ratio.
5. Simplifying the Expression:
- Rearranging gives:
g′=g⋅R2(R+h)2
6. Expanding the Denominator:
- We can express (R+h)2 as:
(R+h)2=R2+2Rh+h2
- Thus, we can write:
g′=g⋅R2R2+2Rh+h2
7. Using Binomial Approximation:
- For small heights h compared to the radius of the Earth R (i.e., h≪R), we can use the binomial approximation:
1(1+2hR+h2R2)≈1−(2hR)
- Therefore:
g′≈g(1−2hR)
8. Final Expression:
- The final expression for the acceleration due to gravity at height h is:
g′=g(1−2hR)
Conclusion:
This expression shows that the acceleration due to gravity decreases linearly with height above the Earth's surface.
- Let g be the acceleration due to gravity at the surface of the Earth.
- Let g′ be the acceleration due to gravity at a height h above the surface.
- Let R be the radius of the Earth.
- The acceleration due to gravity at the surface of the Earth is given by:
g=GMR2
where G is the universal gravitational constant and M is the mass of the Earth.
- At a height h above the surface, the distance from the center of the Earth becomes R+h. Therefore, the expression for g′ at this height is:
g′=GM(R+h)2
- To find the relationship between g′ and g, we can take the ratio:
g′g=GM(R+h)2GMR2=R2(R+h)2
- The GM cancels out in the ratio.
- Rearranging gives:
g′=g⋅R2(R+h)2
- We can express (R+h)2 as:
(R+h)2=R2+2Rh+h2
- Thus, we can write:
g′=g⋅R2R2+2Rh+h2
- For small heights h compared to the radius of the Earth R (i.e., h≪R), we can use the binomial approximation:
1(1+2hR+h2R2)≈1−(2hR)
- Therefore:
g′≈g(1−2hR)
- The final expression for the acceleration due to gravity at height h is:
g′=g(1−2hR)
This expression shows that the acceleration due to gravity decreases linearly with height above the Earth's surface.
Topper's Solved these Questions
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - Revision Exercises (Long Answer Questions)
4 Videos
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - Revision Exercises (Numerical Problems )
19 Videos
- GRAVITATIONBOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - Revision Exercises (Fill in the blanks )
8 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)
12 Videos
Similar Questions
Knowledge Check
The graph that represents variation of g with height (h) from the surface of the earth is
A B
B C
C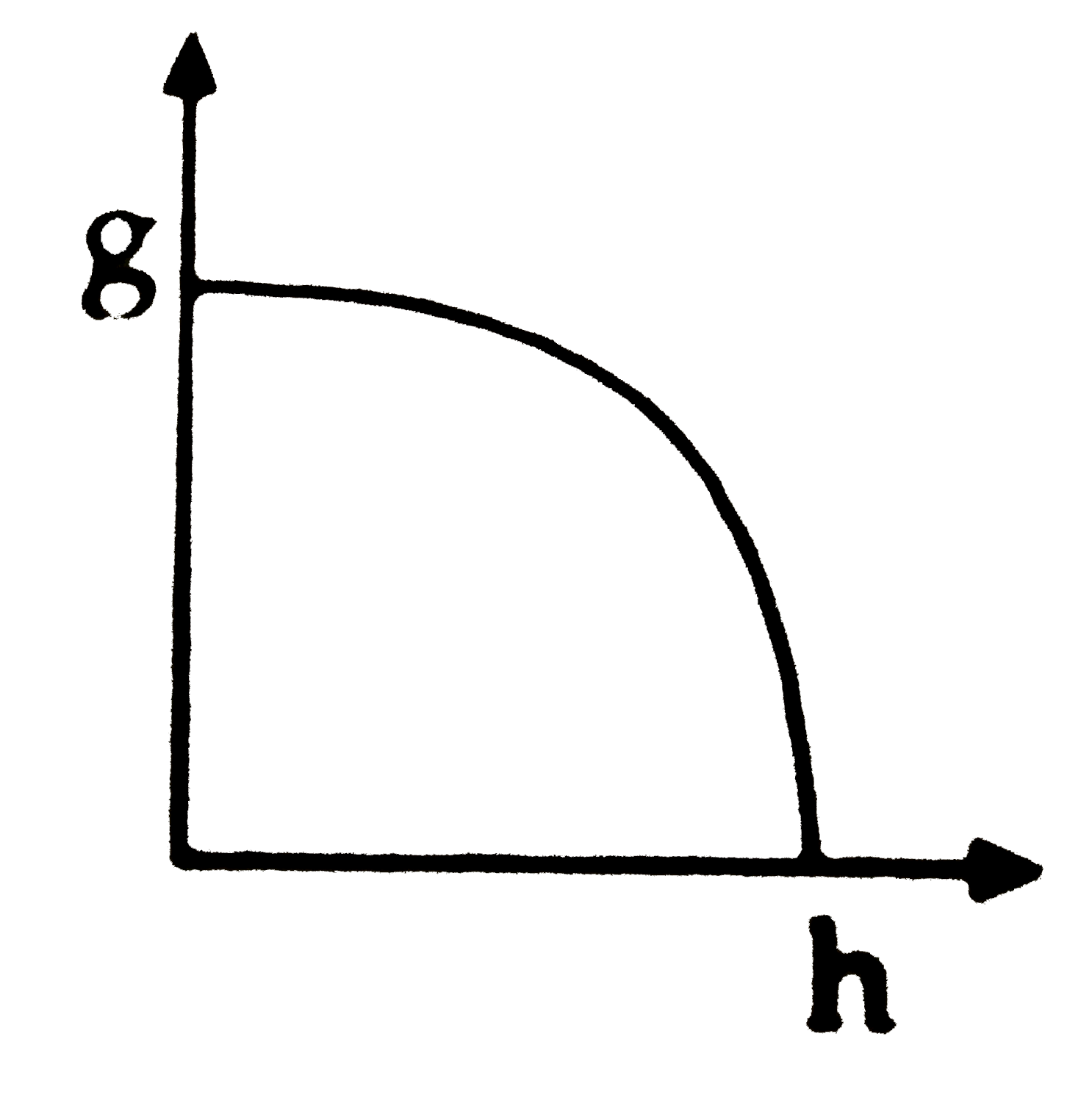 D
D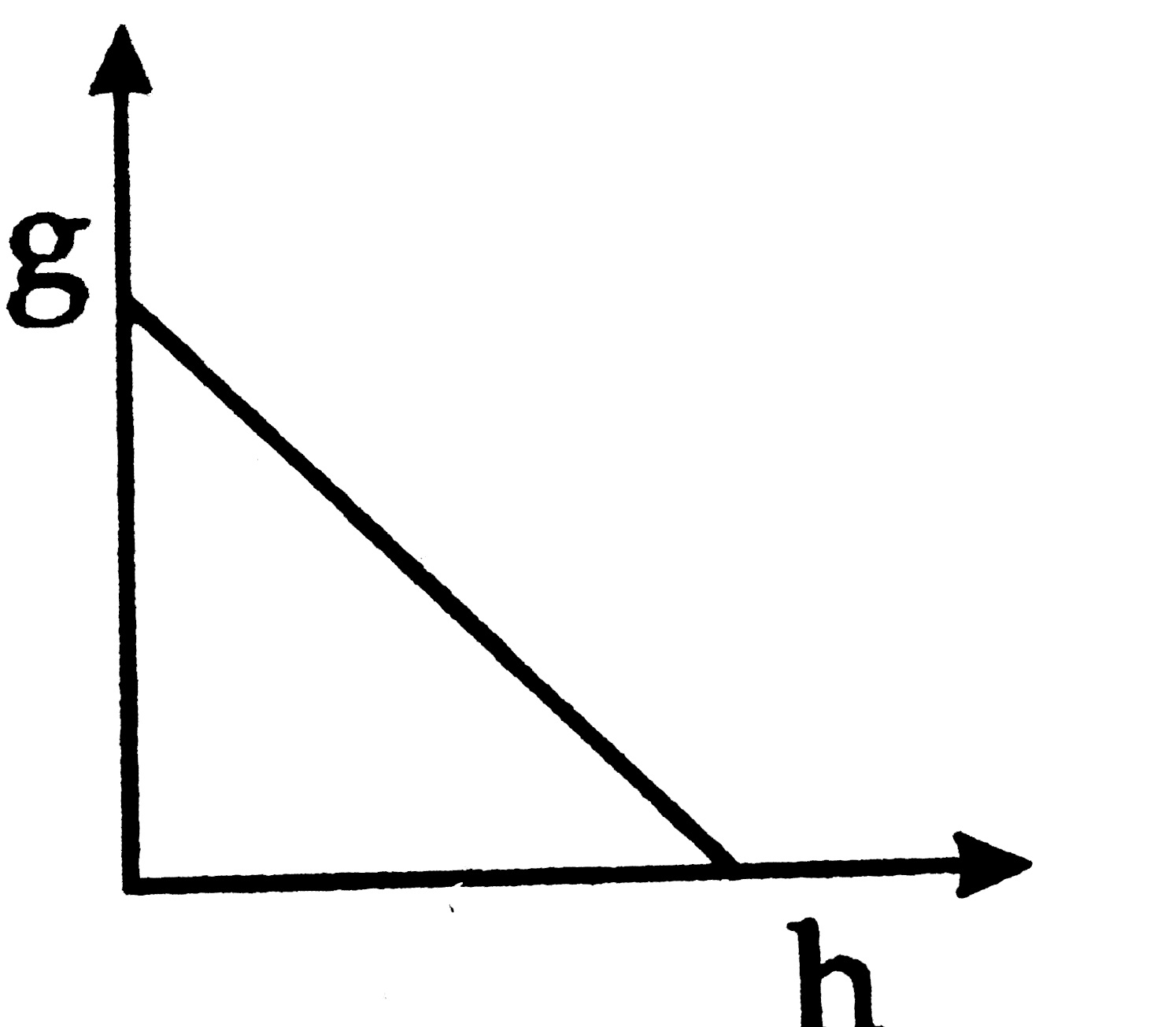
The graph that represents variation of g with depth (d) from the surface of the earth is
A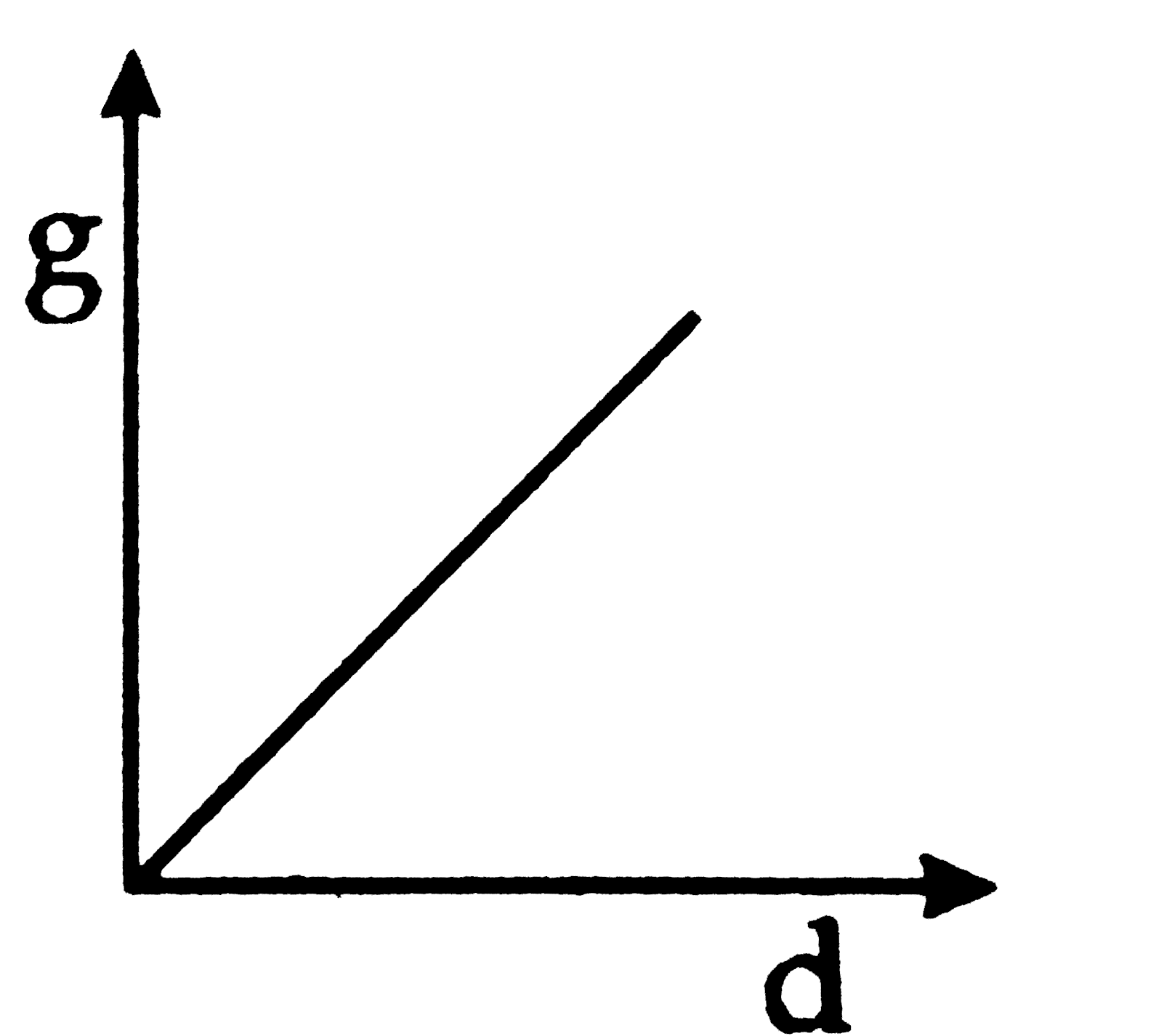 B
B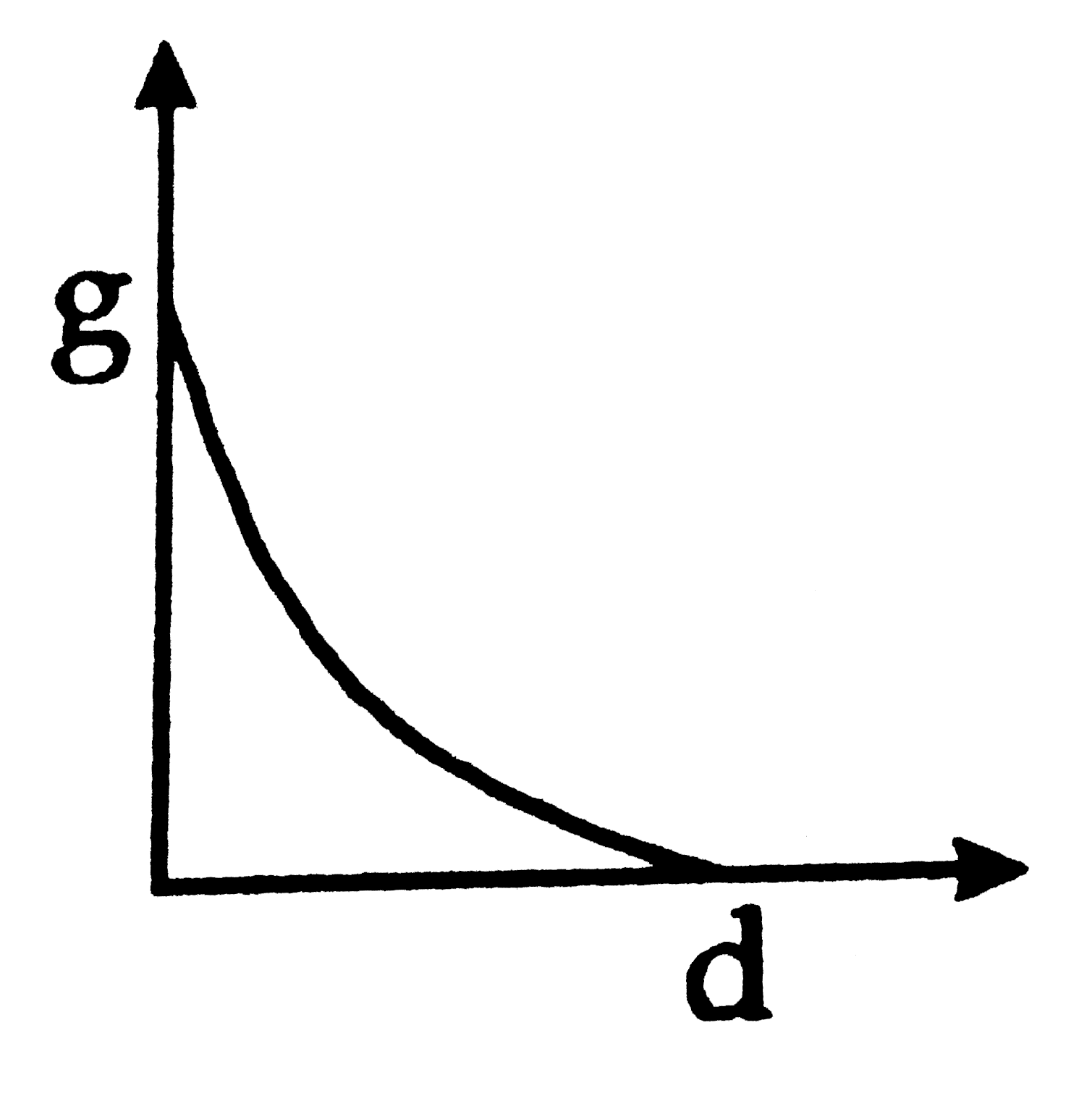 C
C D
D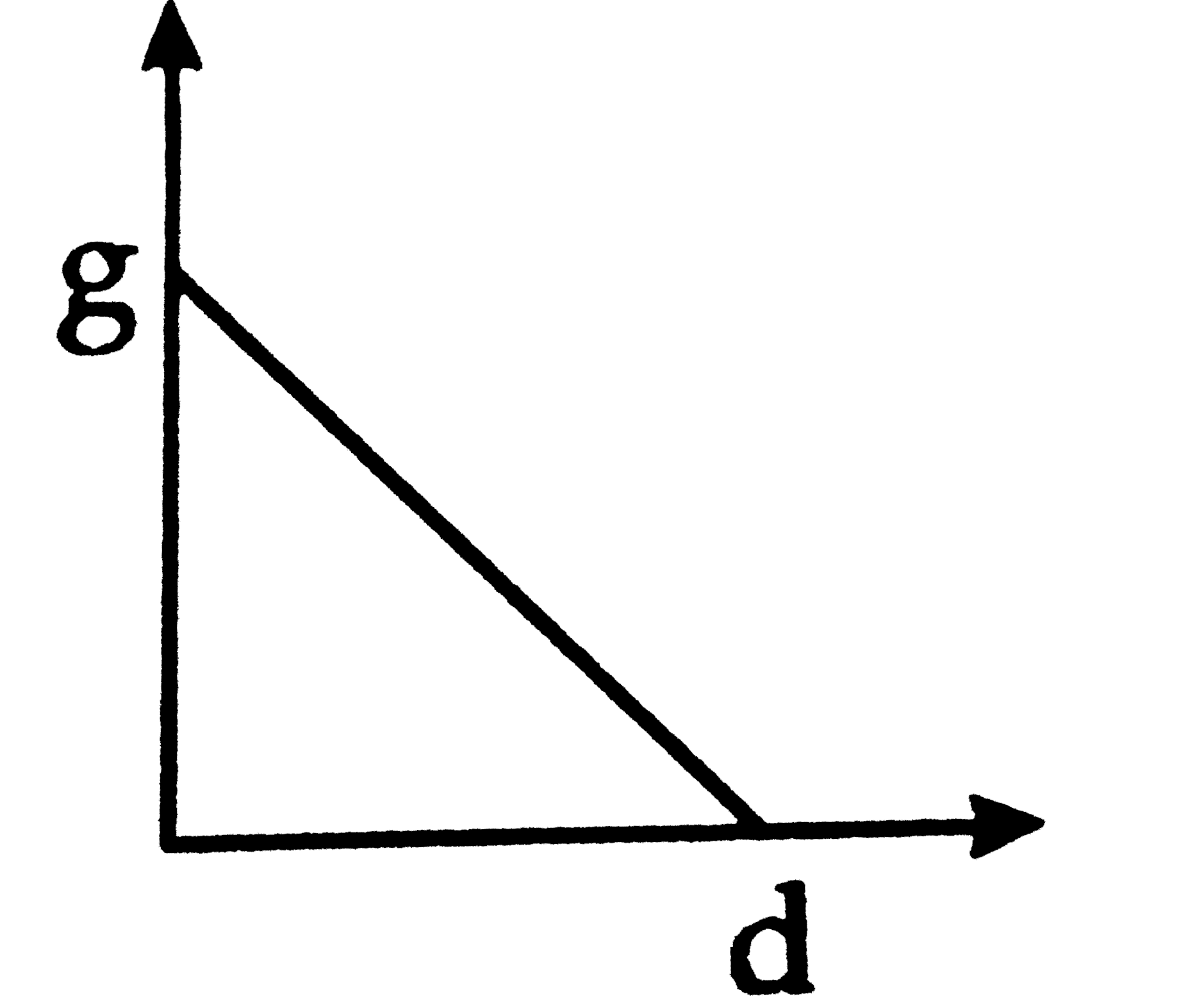
An artificial satellite is placed into a circular orbit around earth at such a height that it always remains above a definite place on the surface of earth. Its height from the surface of earth is
A6400 kmB4800 kmC32000 kmD36000 km
Derive an expression for the escape speed of a body from the surface of the Earth. Express it in terms of the mean density of the Earth.
View SolutionDiscuss the variation of g with height and depth.
View SolutionWhat is the acceleration due to gravity?
View SolutionDraw graphs showing the variation of accleeration due to gravity with (a) height above the Earth's surface, (b) depth below the Earth's surface.
View SolutionObtain an expression for the acceleration due to gravity on the surface of the earth in terms of mass of the earth and its radius. Discuss the variation of acceleration due to gravity with altitude and depth. If a body is taken to a height R / 4 from the surface of the earth, find percentage decrease in the weight of the body ? Here R is the radius of the earth.
View Solution
