A convex lens is placed at a distance of 40 cm from a screen. A point source is placed at a distance of 60 cm from the screen on the same side of the lens. At this position of point-source, a circular spot of light of diameter equal to the lens is formed. Show the formation of image by a ray diagram. Up to what distance the source be displaced so that its clear image can be formed on the screen?
Step-by-Step Solution:
1. Understanding the Setup:
- We have a convex lens placed 40 cm away from a screen.
- A point source is located 60 cm from the screen on the same side as the lens.
2. Identifying Distances:
- Distance from the lens to the screen (v) = 40 cm.
- Distance from the point source to the screen = 60 cm.
- Therefore, the distance from the point source to the lens (u) = 60 cm - 40 cm = 20 cm (on the same side as the lens, hence u = -20 cm).
3. Ray Diagram:
- Draw a ray diagram to illustrate the situation:
- Draw the convex lens.
- Mark the position of the screen.
- Draw rays from the point source to the lens.
- Show how the rays refract through the lens and converge to form an image on the screen.
4. Finding the Focal Length:
- Using the lens formula:
1f=1v−1u
- Substitute the values:
1f=140−1−20
- This simplifies to:
1f=140+120=140+240=340
- Therefore,
f=403≈13.33 cm
5. Finding the New Object Distance for a Clear Image:
- We want to find the new position of the object (u') such that a clear image is formed on the screen.
- Using the lens formula again:
1f=1v−1u′
- Here, v = 40 cm (the distance from the lens to the screen).
- Substitute the values:
1403=140−1u′
- Rearranging gives:
340=140−1u′
- This leads to:
1u′=140−340=−240=−120
- Thus,
u′=−20 cm
6. Calculating the Displacement:
- The original position of the source was at -20 cm (60 cm from the screen).
- The new position of the source is also -20 cm.
- Therefore, the displacement required to form a clear image is:
Displacement=20 cm−13.33 cm=6.67 cm
- The source should be moved towards the lens by approximately 6.67 cm.
- We have a convex lens placed 40 cm away from a screen.
- A point source is located 60 cm from the screen on the same side as the lens.
- Distance from the lens to the screen (v) = 40 cm.
- Distance from the point source to the screen = 60 cm.
- Therefore, the distance from the point source to the lens (u) = 60 cm - 40 cm = 20 cm (on the same side as the lens, hence u = -20 cm).
- Draw a ray diagram to illustrate the situation:
- Draw the convex lens.
- Mark the position of the screen.
- Draw rays from the point source to the lens.
- Show how the rays refract through the lens and converge to form an image on the screen.
- Using the lens formula:
1f=1v−1u
- Substitute the values:
1f=140−1−20
- This simplifies to:
1f=140+120=140+240=340
- Therefore,
f=403≈13.33 cm
- We want to find the new position of the object (u') such that a clear image is formed on the screen.
- Using the lens formula again:
1f=1v−1u′
- Here, v = 40 cm (the distance from the lens to the screen).
- Substitute the values:
1403=140−1u′
- Rearranging gives:
340=140−1u′
- This leads to:
1u′=140−340=−240=−120
- Thus,
u′=−20 cm
- The original position of the source was at -20 cm (60 cm from the screen).
- The new position of the source is also -20 cm.
- Therefore, the displacement required to form a clear image is:
Displacement=20 cm−13.33 cm=6.67 cm
- The source should be moved towards the lens by approximately 6.67 cm.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - PRACTICE PROBLEMS (1)13videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - PRACTICE PROBLEMS (2)9videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION15videos
NUCLEI
- BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION12videos
SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS
Similar Questions
In Fig. a convex, lens L is placed at a distance of 36 cm from a screen. If a point-source P is placed at 56 cm from the screen then a circular spot of light of diameter equal to the diameter of the lens is formed. Show the image formation by a ray diagram. Calculate upto what distance the source be displaced so that its clear image can be formed on the screen.
 View Solution
View SolutionAn object is placed at a distance of 30 cm from a convex lens of focal length 20 cm.Find the position of the image .
View Solution
Knowledge Check
- Question 1 - Select One
An illuminated object is placed at a distance of 20 cm from a converging lens of focal length 15 cm. The image obtained on the screen is:
Aupright and magnifiedBinverted and magnifiedCinverted and diminishedDupright and diminished. - Question 2 - Select One
An object is placed at a distance of 20 cm from a convex lens of focal length 10 cm . The image is formed on the other side of the lens at a distance
A20 cmB10 cmC40 cmD30 cm - Question 3 - Select One
An object is kept at a distance of 15 cm from a convex lens of focal length 10 cm. Calculate the image distance and state the characteristics of the image formed.
Aupright and magnifiedBinverted and magnifiedCinverted and diminishedDupright and diminished
An object is placed at 10 cm from a convex lens of focal length 12 cm. Find the position, nature and magnification of the image.
View SolutionA luminous object is placed at a distance of 40 cm from a converging lens of focal length 25 cm. The image obtained in the screen is
View SolutionFig. shows a plane mirror M placed at a distance of 10cm from a concave lens L. A point object is placed at a distance of 60cm from the lens. The image formed due to refraction by the lens and reflection by the mirror is 30cm behind th mirror. What is the focal length of this lens ?
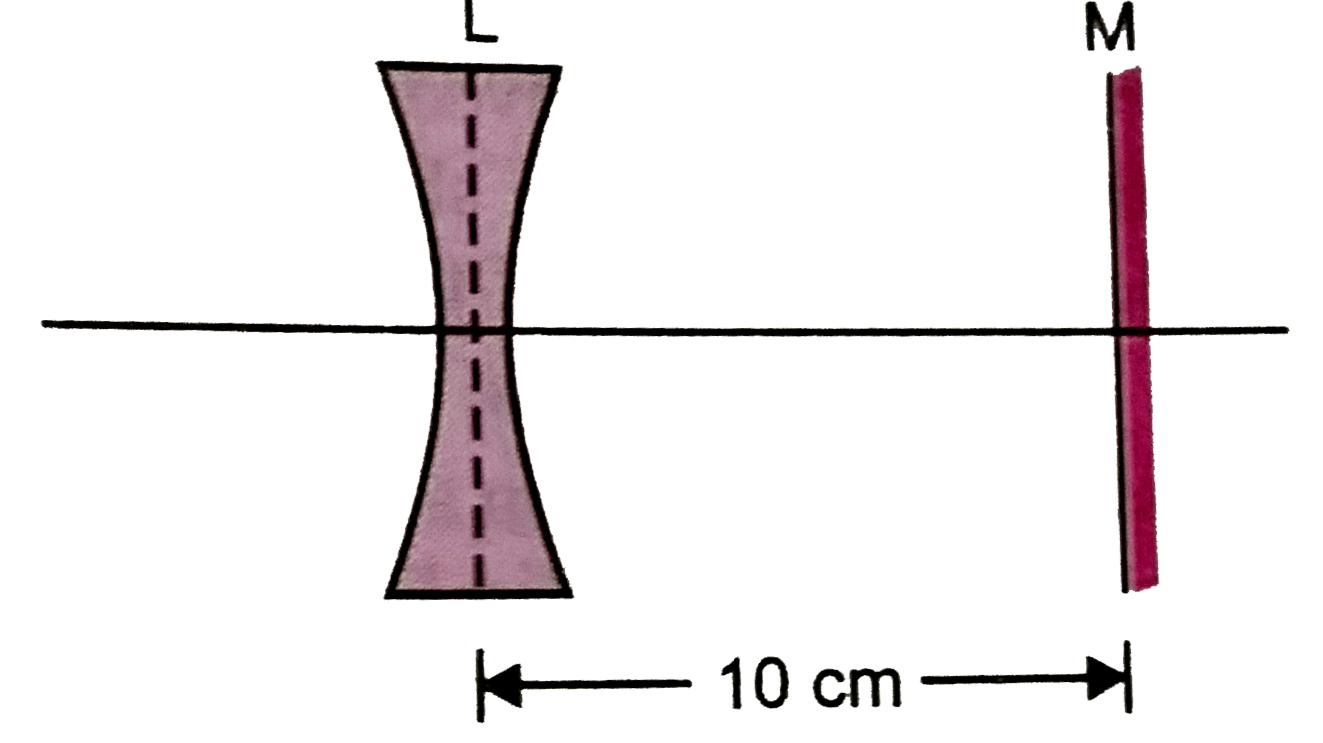 .View Solution
.View SolutionAn illuminated object is placed at a distance of 20 cm from a converging lens of focal length 15 cm. The image obtained on the screen is:
View SolutionAn object is placed at a distance of 40 cm from a convex lens and its real and inverted image of same size is formed on a screen placed on other side of lens. The focal length of lens is
View Solution

