The inner bottom of a tub filled with water is stained with a mark. The water is filled to a height of 7 cm. Calculate the distance by which the stain appears to be raised. Refractive index of water is 1.33.
To solve the problem of how much the stain appears to be raised when viewed from above the water surface, we can use the concept of apparent depth due to refraction. Here’s a step-by-step solution:
Step 1: Understand the Problem
We have a tub filled with water to a height of 7 cm, and we need to find out how high the stain appears to be raised due to the refraction of light at the water-air interface.
Step 2: Identify Given Values
- Actual depth of water (T) = 7 cm
- Refractive index of air (μ1) = 1 (approximately)
- Refractive index of water (μ2) = 1.33
Step 3: Use the Formula for Apparent Depth
The relationship between the actual depth (T) and the apparent depth (T') can be given by the formula:
T′μ1=Tμ2
From this, we can rearrange to find T':
T′=T⋅μ1μ2
Step 4: Substitute the Values
Substituting the known values into the equation:
T′=7cm⋅11.33
Step 5: Calculate T'
Now, perform the calculation:
T′=7cm⋅0.7519≈5.26cm
Step 6: Calculate the Shift in Depth
The shift in depth (ΔT) is given by:
ΔT=T−T′
Substituting the values:
ΔT=7cm−5.26cm
Step 7: Perform the Final Calculation
Calculating the shift:
ΔT=1.74cm
Conclusion
The stain appears to be raised by approximately 1.74 cm.
---
We have a tub filled with water to a height of 7 cm, and we need to find out how high the stain appears to be raised due to the refraction of light at the water-air interface.
- Actual depth of water (T) = 7 cm
- Refractive index of air (μ1) = 1 (approximately)
- Refractive index of water (μ2) = 1.33
The relationship between the actual depth (T) and the apparent depth (T') can be given by the formula:
T′μ1=Tμ2
From this, we can rearrange to find T':
T′=T⋅μ1μ2
Substituting the known values into the equation:
T′=7cm⋅11.33
Now, perform the calculation:
T′=7cm⋅0.7519≈5.26cm
The shift in depth (ΔT) is given by:
ΔT=T−T′
Substituting the values:
ΔT=7cm−5.26cm
Calculating the shift:
ΔT=1.74cm
The stain appears to be raised by approximately 1.74 cm.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - PRACTICE PROBLEMS (3)
18 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - PRACTICE PROBLEMS (4)
6 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - PRACTICE PROBLEMS (1)
13 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
12 Videos
Similar Questions
Knowledge Check
What is the real depth of a swimming pool when its bottom appears to be raised by 1 m ? Given refractive index of water is 4/3.
A2mB16mC4mD8mA tank of height 50 m is filled with oil fully. If the bottom of the tank appears to be 40 m below its top, the refractive index of the oil should be
A45B15C14D54There is a hole h metre from its top of a tank filled with water. Calculate the distance x where the stream of water will touch the ground from the bottom (in m).
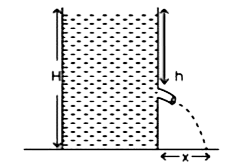 A2√h(H−h)B2√g(H−h)C√2hHD√2gH
A2√h(H−h)B2√g(H−h)C√2hHD√2gH
The depth of water in a bucket is 40 cm but its bottom appears to be raised by 10 cm. what is the refractive index of water ?
View SolutionFor a fish under water, what will be the height of a person whose actual height is 6 feet? Refractive index of water is 1.33?
View SolutionA coin placed at the bottom of a tank appears to be raised when water is poured into it. Explain.
View SolutionThe ratio of velocities of light in glass that in whater is ( refractive inde of glaass = 1.5 and refractive index of water = 1. 33)
View SolutionA thin hollow prism of refracting angle 3°, filled with water gives a deviation of 1°. The refractive index of water is
View Solution
