A small LED, emitting light is placed at x distance above a spherical glass of refractive index 1.5 and radius of curvature 30 cm. The image of the LED is formed at a distance of 150 cm away from the surface of sphere along the direction of incident light. Calculate the distance between LED light and the surface of spherical glass.
To solve the problem, we will use the lens maker's formula for refraction at a spherical surface. The formula we will use is:
n2−n1R=n2v−n1u
Where:
- n1 = refractive index of the first medium (air) = 1
- n2 = refractive index of the second medium (glass) = 1.5
- R = radius of curvature of the spherical surface = 30 cm (positive since the center of curvature is on the same side as the incoming light)
- v = image distance = 150 cm (positive since the image is formed on the same side as the outgoing light)
- u = object distance (which we need to find)
Step 1: Substitute the known values into the formula
Substituting the values into the formula, we have:
1.5−130=1.5150−1u
Step 2: Simplify the left side
The left side simplifies to:
0.530=1.5150−1u
Calculating 0.530:
0.530=160
Step 3: Simplify the right side
Now calculate 1.5150:
1.5150=1100
So the equation now looks like:
160=1100−1u
Step 4: Rearrange the equation to find 1u
Rearranging gives us:
1u=1100−160
Step 5: Find a common denominator
The common denominator of 100 and 60 is 300. Rewriting the fractions:
1100=3300,160=5300
Thus:
1u=3300−5300=−2300
Step 6: Solve for u
Taking the reciprocal gives:
u=−3002=−150 cm
Step 7: Interpret the result
The negative sign indicates that the object (LED) is located 150 cm above the surface of the spherical glass in the direction opposite to the incident light.
Conclusion
The distance between the LED light and the surface of the spherical glass is:
Distance=150 cm
- n1 = refractive index of the first medium (air) = 1
- n2 = refractive index of the second medium (glass) = 1.5
- R = radius of curvature of the spherical surface = 30 cm (positive since the center of curvature is on the same side as the incoming light)
- v = image distance = 150 cm (positive since the image is formed on the same side as the outgoing light)
- u = object distance (which we need to find)
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - PRACTICE PROBLEMS (5)
3 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - PRACTICE PROBLEMS (6)
3 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - PRACTICE PROBLEMS (3)
18 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
12 Videos
Similar Questions
A double convex spherical glass has refractive index 1.5 and both radius of curvature 30 cm. A point object is placed at a distance of 120 cm from the spherical glass. What will be the position of the image formed ?
View SolutionLight from a point source in air falls on a spherical glass surface μ=1.5andR=20cm. The image is formed at a distance of 100cm from the glass surface in the direction of incident light. Calculate the object distance from the centre of curvature of the spherical surface.
View Solution
Knowledge Check
A point object O is placed in front of a glass rod having spherical end of radius of curvature 30cm. The image would be formed at
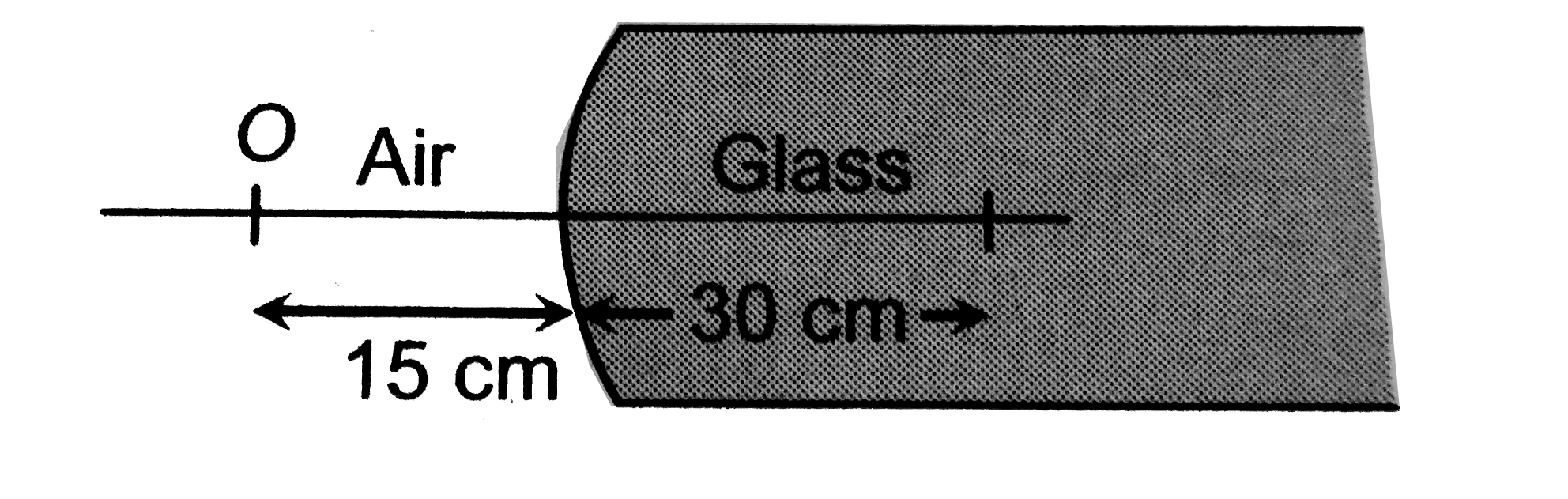 A30 cm lefBinfinityC1 cm to the rightD18 cm to the left
A30 cm lefBinfinityC1 cm to the rightD18 cm to the leftAn image is formed at a distance of 100 cm from the glass surface with refractive index 1.5, when a point object is placed in the air at a distance of 100 cm from the glass surface. The radius of curvature is of the surface is
A20 cmB40 cmC30 cmD50 cmA denser medium of refractive index 1.5 has a concave surface of radius of curvature 12 cm. An object is situated in the denser medium at a distance of 9 cm from the pole. Locate the image due to refraction in air.
AA real image at 8 cmBA virtual image at 8 cmCA real image at 4.8 cmDA virtual image at 4.8 cm
A double convex lens made of glass of refractive index 1.56 has both radii of curvature of magnitude 20cm. If an object is placed at a distance of 10cm from this lens, find the position of image formed.
View SolutionLight from a point source in air falls on a spherical glass surface (n = 1.5 and radius of curvature = 20 cm). The distance of the light source from the glass surface is 100 cm. At what position the image is formed ?
View SolutionA small point object is placed atOat a distance of0.60metre in air from a convex spherical surface of refractive index1.5.If the radius of the curvature is 25cmthen what is the position of the image on the principal axis.
View SolutionFrom a point source a light falls on a spherical glass surface (μ=1.5 and radius of curvature =10cm). The distance between point source and glass surface is 50cm. The position of image is
View SolutionThe distance travelled by light in glass (refractive index =1.5) in a nanosecond will be
View Solution
