There is one cylindrical vessel whose height and diameter are both equal to D. An observer's eye is placed in such a manner that bottom edge of the vessel is just visible to eye.
$There is one cylindrical vessel whose height and diameter are both equal to D. An observer's eye is placed in such a manner that bottom edge of the vessel is just visible to eye. There is a point P at the bottom of container at a distance x from the centre of container as shown in the figure. Up to what height the liquid of refractive index mu should be poured in the vessel so that point P is visible to the eye?$
There is a point P at the bottom of container at a distance x from the centre of container as shown in the figure. Up to what height the liquid of refractive index $μ$ should be poured in the vessel so that point P is visible to the eye?

Text Solution

Verified by Experts

From the figure given below we can understand that he need to put liquid up to a height so that after refraction from liquid up to a height so that after refraction from liquid light ray from point P is refracted along the line of vision . Line of vision of eye is at $45^{\circ}$ because we know that height and diameter of vessel both are equal to D . Let h be the height of liquid poured.

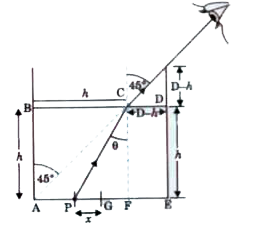
We can see in the figure that the angle of incidence of light ray from point P is equal to $θ$ . Let us apply Snell.s law at point C in the diagram .
$μ sin θ = {sin 45}^{\circ}$
$sin θ = \frac{1}{μ \sqrt{2}} ... (i)$
Further from the figure we can write the following :
PF = PE - FE
$\Rightarrow P F = (D / 2 + x) - (D - h)$
$\Rightarrow P F = x + h - D / 2 ... (i i)$
Further from the figure we can write the following :
$tan θ = \frac{P F}{C F}$
$\Rightarrow tan θ = \frac{x + h - \frac{D}{2}}{h} ... (i i i)$
Now from equation (i) we can write the following :
$tan θ = \frac{1}{\sqrt{2 μ^{2} - 1}} ... (i v)$
From equation (iii) and (iv) we can write the following :
From equation (iii) and (iv) we can write the following :
$\frac{x + h - \frac{D}{2}}{h} = \frac{1}{\sqrt{2 μ^{2} - 1}}$
$\Rightarrow \frac{2 x + 2 h - D}{2 h} = \frac{1}{\sqrt{2 μ^{2} - 1}}$
$\Rightarrow (2 x - D) (\sqrt{2 μ^{2} - 1}) + 2 h (\sqrt{2 μ^{2} - 1}) = 2 h$
$\Rightarrow (2 x - D) (\sqrt{2 μ^{2} - 1}) = 2 h (1 - \sqrt{2 μ^{2} - 1})$
$\Rightarrow h = \frac{(2 x - D) (\sqrt{2 μ^{2} - 1})}{2 (1 - \sqrt{2 μ^{2} - 1})}$

Updated on:21/07/2023

A rectangular vessel of dimension ( $l \times b \times h$ ) and mass $M$ contains a liquid of density $ρ$ . The vessel has an orifice at its bottom at a distance $c$ from the rear wall as shown in the figure.

AThe maximum volume of the water that can be stored when the vessel is accelerated is $h c b / 2$
BThe maximum volume of the water that can be stored when the vessel is accelerated is $h l b / 2$
CForce F that must he applied when maximum water stored is $[M + \frac{h c b ρ}{2}] \frac{h g}{c}$
DForce F that must be applied when maximum water stored is $[M + \frac{h c b ρ}{2}] \frac{l g}{c}$
The height to which a cylindrical vessel be filled with a homogenous liquid, to make the average force with which the liquid presses the side of the vessel equal to the force exerted by the liquid on the bottom of the vessel, is equal to.
Ahalf of the radius of the vessel
Bradius of the vessel
Cone-fourth of the radius of the vessel
Dthree-fourth of the radius of the vessel.
There is a hole of area $\frac{1}{25} c m^{2}$ in the bottom of a cylindrical vessel containing fluid up to height $h$ . The liquid flows out in time $t$ . If the liquid were filled in the vessel up to height $4 h$ , then it would flow out in time
At
B2t
C4t
D $\frac{t}{2}$