Fig. shows an equiconvex lens (of refractive index 1.5) in contact with a liquid layer on top of a plane mirror. A small needle with its tip on the principal axis is moved along the axis until its inverted image is found at the position of the needle. The distance of the needle from the lens is measured to be 45.0cm. The liquid is removed and the experiment is repeated. The new distance is measured to be 30.0cm. What is the refractive index of the liquid ?
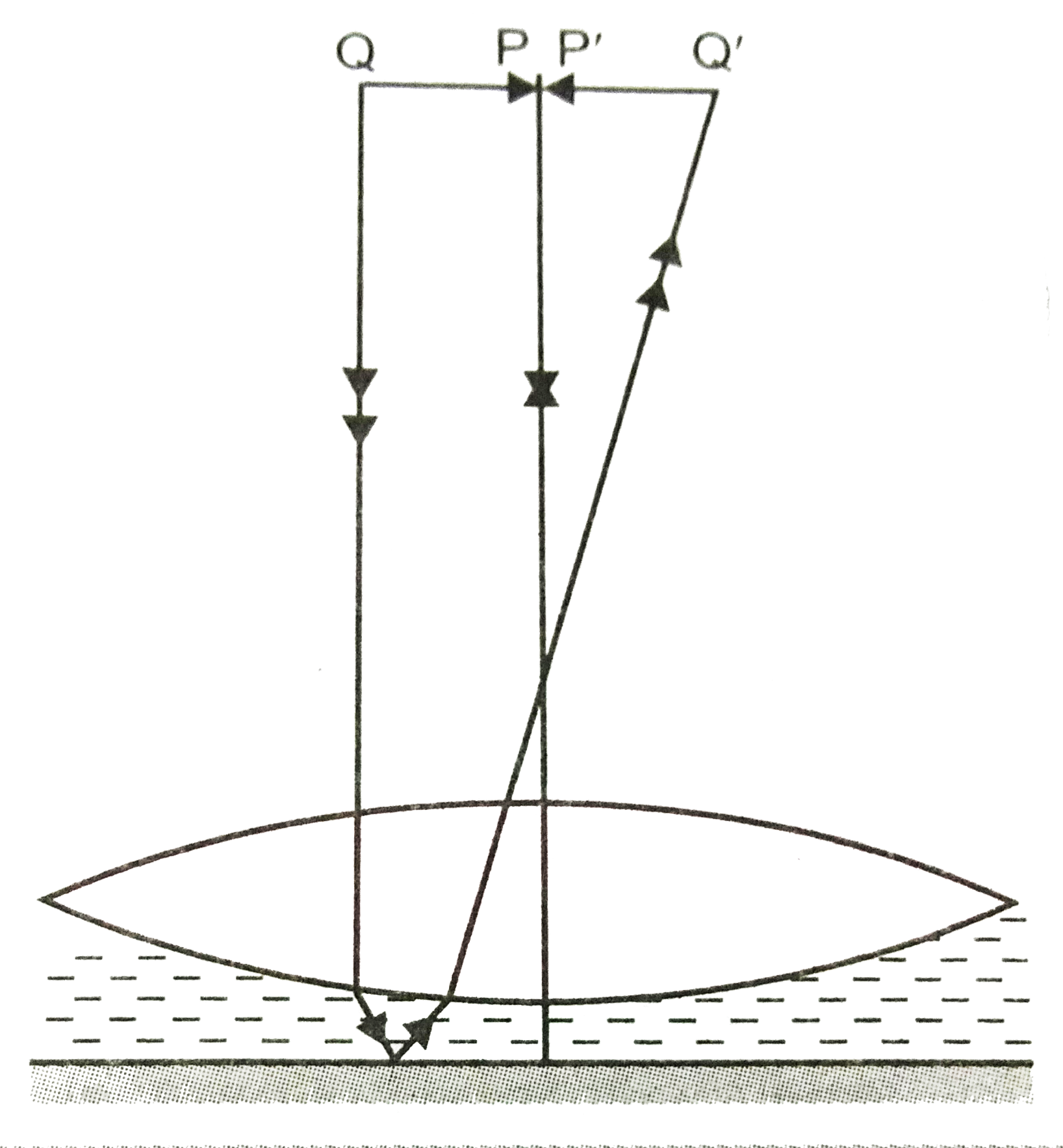
Here, refractive index of convex lens, μ=1.5.
Let μ1 be the refractive index of liquid.
When the liquid is present, the system behaves as a combination of the convex lens (μ) and plano-concave lens of liquid (μ1).
So, in this case, the distance of the needle from the lens, for which the inverted image is found at the position of needle itself, is equal to the combined focal length of the convex lens and plano-concave lens of liquid.
∴ f=45cm
When liquid is removed, then f1=30cm is focal length of convex lens only. If f2 is focal length of plano - concave liquid lens, then from 1f1+1f2=1f
1f2=1f−1f1
=145−130=2−390
or 1f2=−190
f2=−90cm
Using lens maker.s formula for equiconvex lens where in
R1=RandR2=−R
1f1=(μ−1)(1R1+1R2)
130=(1.5−1)(1R+1R)
=12×2R=1R
R=30cm
For plano - concave lens of liquid.
f2=−90cm,μ=?
R1=−30cm (for plane surface)
R2=∞
As 1f2=(μ1−1)(1R1−1R2)
∴ −190=(μ1−1)(1−30−1∞)
−190=μ1−1−30
μ1−1=−30−90=13
μ1=13+1=43=1.33
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - NCERT (EXemplar Problems Obejective Questions) (Multiple Choice Questions (Type-I)10videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - NCERT (EXemplar Problems Obejective Questions) (Multiple Choice Questions (Type-II)6videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Tough & Tricky (PROBLEMS)20videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION15videos
NUCLEI
- BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION12videos
SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS
Similar Questions
Fig. 9.12 shows an equiconvex lens (of refractive index 1.50) in contact with a liquid layer on top of a plane mirror. A small needle with its tip on the principal axis is moved along the axis until its inverted image is found at the position of the needle. The distance of the needle from the lens is measured to be 45.0 cm. The liquid is removed and the experiment is repeated. The new distance is measured to be 30.0 cm. What is the refractive index of the liquid ?
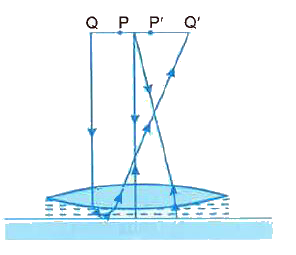 View Solution
View SolutionAn equiconvex lens, with redii of curvature of magnitude 10cm each, is put over a liquid layer poured on top of a plane mirror. A small needle, with its tip on the principal axis of the lens, is moved along the axis until its inverted real image coincides with the needle itself. The distance of the needle, from the lens, is measured to be 15cm .
On removing the liquid layer, and repeating the experiment the distance is measured to be 10cm . Given that the two values of the distance measured represent the force length values in the two cases, calculate the refractive index of the liqiud.View SolutionAn equiconvex lens with radii of curvature of magnitude R each is put over a liquid layer poured on top of a plane mirror. A small needle, with its tip on the principal axis of the lens, is moved along the axis until its inverted real image coincides with the needle itself. The distance of the needle from the lens is measured to be 'a'. On removing the liquid layer and repeating the experiment the distance is found to be 'b'.
Given that the two values of distances measured represent the focal length values in the two cases, obtain a formula for the refractive index of the liquid.
 View Solution
View SolutionA symmetric biconvex lens of radius of curvature R and made of glass of refractive index 1.5, is placed on a layer of liquid placed on top of a plane mirror as shown in the figure. An optical needle with its tip on the principal axis of the lens is moved along the axis until its real, inverted image coincides with the needle itself. The distance of the needle from the lens is measured to be x. On removing the liquid layer and repeating the experiment, the distance is found to be y. Obtain the expression for the refractive index of the liquid in terms of x and y.
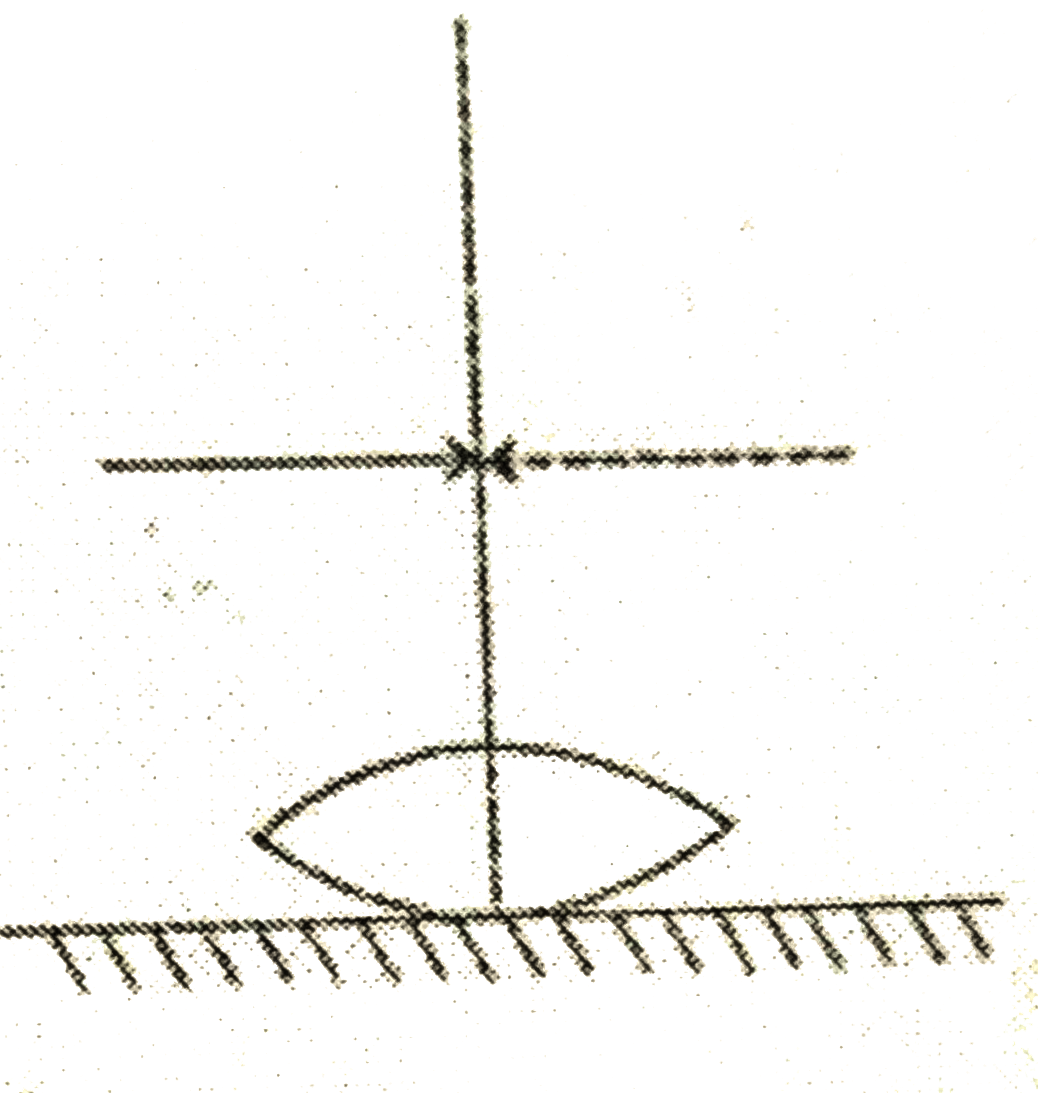 View Solution
View SolutionA synunetdc bionvex fens of radius of curvature Rand made of glass of refractive index 1.5, is placed on a placed on top of a plane mirror as shown in the figure.An optical needle with with its tip on the principal axis of the lens is moved along the axis until its real, inverted images conicides with the needle itself. The distance from the lens in measured to be x. On removing the liquid layer and repeating the experiment, the distance is found to be y . Obtain the expression for the refractive index of the liquid in terms of x and y.
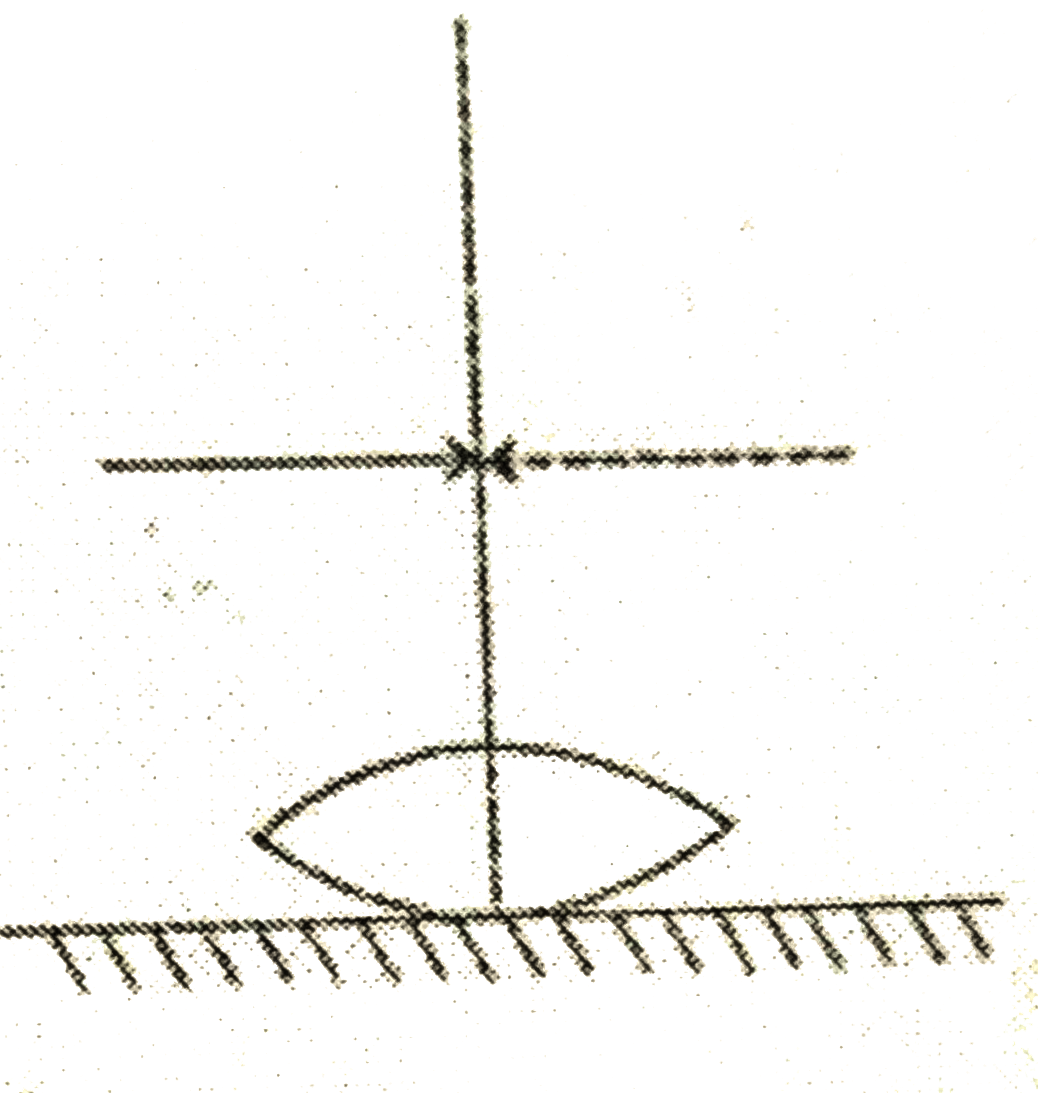 View Solution
View SolutionAn equiconvex lens with radii of curvature of magnitude R each is put over a liquid layer poured on top of a plane mirror. A small needle, with its tip on the principal axis of the lens, is moved along the axis until its inverted real image coincides with the needle itself. The distance of the needle from the lens is measured to be 'a'. On removing the liquid layer and repeating the experiment the distance is found to be 'b'.
Given that the two values of distances measured represent the focal length values in the two cases, obtain a formula for the refractive index of the liquid.
 View Solution
View SolutionAn equiconvex lens with radii of curvature of magnitude R each is put over a liquid layer poured on top of a plane mirror. A small needle, with its tip on the principal axis of the lens, is moved along the axis until its inverted real image coincides with the needle itself. The distance of the needle from the lens is measured to be 'a'. On removing the liquid layer and repeating the experiment the distance is found to be 'b'.
Given that the two values of distances measured represent the focal length values in the two cases, obtain a formula for the refractive index of the liquid.
 View Solution
View SolutionA glass lens of refractive index 1.45 disappears when immersed in a liquid. What is the value of refractive index of the liquid ?
View SolutionA needle 10 cm long is placed along the axis of a convex lens of focal length 10 cm such that the middle point of the neddle is at a distance of 10 cm from the lens. Find the length of the image of the neddle.
View SolutionAn object 50cm tall is placed on the principal axis of a convex lens. Its 20cm tall image is formed on the screen placed at a distance of 10cm from the lens. Calculate the focal length of the lens.
View Solution
