When a person moves towards a mirror with velocity 3v, by which velocity his image moves relative to himself ?
To solve the problem of finding the velocity of the image relative to the person moving towards the mirror, we can follow these steps:
Step 1: Understand the scenario
A person is moving towards a mirror with a velocity of 3v. When a person moves towards a mirror, their image also moves towards them, but at a different rate.
Step 2: Determine the velocity of the image
When the person moves towards the mirror with a velocity of 3v, the image of the person in the mirror will also move towards the person at the same speed 3v. This is because the image in a plane mirror is always at the same distance behind the mirror as the person is in front of it.
Step 3: Calculate the relative velocity
To find the velocity of the image relative to the person, we need to consider both velocities. The person is moving towards the mirror at 3v and the image is also moving towards the person at 3v.
- Let vp be the velocity of the person: vp=3v (towards the mirror).
- Let vi be the velocity of the image: vi=3v (towards the person).
Step 4: Use the formula for relative velocity
The relative velocity of the image with respect to the person can be calculated using the formula:
vrelative=vi−(−vp)
Since the person is moving towards the mirror, we consider their velocity as negative in this context. Thus:
vrelative=vi+vp=3v+3v=6v
Final Answer
The velocity of the image relative to the person is 6v.
---
A person is moving towards a mirror with a velocity of 3v. When a person moves towards a mirror, their image also moves towards them, but at a different rate.
When the person moves towards the mirror with a velocity of 3v, the image of the person in the mirror will also move towards the person at the same speed 3v. This is because the image in a plane mirror is always at the same distance behind the mirror as the person is in front of it.
To find the velocity of the image relative to the person, we need to consider both velocities. The person is moving towards the mirror at 3v and the image is also moving towards the person at 3v.
- Let vi be the velocity of the image: vi=3v (towards the person).
The relative velocity of the image with respect to the person can be calculated using the formula:
vrelative=vi−(−vp)
Since the person is moving towards the mirror, we consider their velocity as negative in this context. Thus:
vrelative=vi+vp=3v+3v=6v
The velocity of the image relative to the person is 6v.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Revision Exercises (Additional Questions)
22 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Revision Exercises (Fill in the Blanks)
10 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Higher Order Thinking Skills & Advanced Level (QUESTIONS WITH ANSWERS)
20 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
12 Videos
Similar Questions
By the term velocity of rain, we mean velocity with which raindrops fall relative to the ground. In absence of wind, raindrops fall vertically and in presence of wind raindrops fall obliqucly. Moreover raindrops acquire a constant terminal velocity due air resistance very quickly as they fall toward the carth. A moving man relative to himself observes an altered velocity of raindrops. Which is known as velocity of rain relative to the man. It is given by the following equation.
→vrm=→vr−→vm
A standstill man relative to himself observes rain falling with velocity, which is equal to velocity of the raindrops relative to the ground. To protect himself a man should his umbrella against velocity of raindrops relative to himself as shown in the following figure.

Rain is falling vertically with velocity 80 cm/s.
(a) How should you hold your umbrella ?
(b) You start walking towards the east with velocity 60 cm/s. How should you hold umbrella ?
(c) You are walking towards the west with velocity 60 cm/s. How should you hold your umbrella ?
(d) You are walking towards the north with velocity 60 cm/s. How should you hold your umbrella?
(e) You are walking towards the south with velocity 80 cm/s. How should you hold your umbrella ?
View SolutionBlock B moves to the right with a constant velocity v0. The velocity of body A relative to B is :
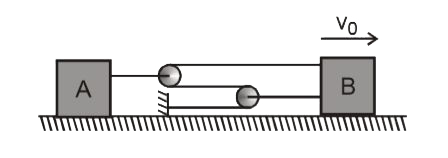
View Solution
Knowledge Check
A person moves with a velocity v towards a plane mirror. With what velocity does his image move towards him ?
A3vB2vC4vDv2A plane mirror and a person are moving towards each other with same velocity v. Then the velocity of the image is
AvB2vC3vD4vSTATEMENT -1 : when an object moves towards a plane mirror with a certain velocity, its image will also move with same velocity.
and
STATEMENT - 2 : The distance from mirror to image is equal to distance of object from mirror.AStatement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-10BStatement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-11CStatement-1 is True, Statement-2 is falseDStatement-1 is False, Statement-2 is True
By the term velocity of rain, we mean velocity with which raindrops fall relative to the ground. In absence of wind, raindrops fall vertically and in presence of wind raindrops fall obliqucly. Moreover raindrops acquire a constant terminal velocity due air resistance very quickly as they fall toward the carth. A moving man relative to himself observes an altered velocity of raindrops. Which is known as velocity of rain relative to the man. It is given by the following equation.
→vrm=→vr−→vm
A standstill man relative to himself observes rain falling with velocity, which is equal to velocity of the raindrops relative to the ground. To protect himself a man should his umbrella against velocity of raindrops relative to himself as shown in the following figure.

When you are standstill in rain, you have to hold umbrella vertically to protect yourself.
(a) When you walk with velocity 90 cm/s, you have to hold your umbrella at 53∘ above the horizontal. What is velocity of the raindrops relative to the ground and relative to you ?
(b) If you walk with speed 160 cm/s, how should you hold your umbrella ?
View SolutionAs an object moves towards a convex mirror, the image
View SolutionTwo identical particles move towards each other with velocity 2v and v, respectively. The velocity of the centre of mass is:
View SolutionTwo identical particles move towards each other with velocity 2v and v respectively. The velocity of centre of mass is
View SolutionBlock B moves to the right with a constant velocity v0. The velocity of body A relative to B is
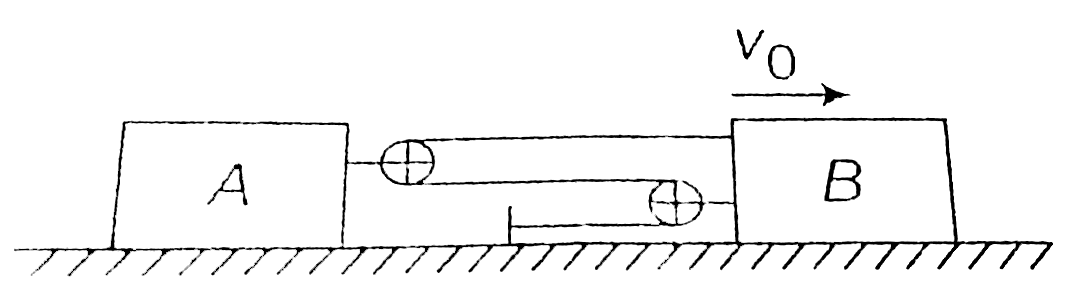
View Solution
