For what angle of incidence, the lateral shift produced by a parallel sided glass plate is maximum ?
The correct Answer is:B
To determine the angle of incidence at which the lateral shift produced by a parallel-sided glass plate is maximum, we can follow these steps:
Step 1: Understand Lateral Shift
Lateral shift (S) is defined as the horizontal displacement of a light ray as it passes through a parallel-sided glass plate. It can be calculated using the formula:
S=t⋅secR⋅sin(I−R)
where:
- t = thickness of the glass plate
- I = angle of incidence
- R = angle of refraction
Step 2: Analyze the Formula
To maximize the lateral shift S, we need to maximize both secR and sin(I−R).
Step 3: Relate Angles Using Snell's Law
According to Snell's Law:
n1sinI=n2sinR
where n1 is the refractive index of air (approximately 1) and n2 is the refractive index of glass.
Step 4: Determine Maximum R
The angle of refraction R will be maximum when the angle of incidence I is also maximized. The maximum angle of incidence occurs when the light ray is incident parallel to the surface of the glass plate, which corresponds to the critical angle condition.
Step 5: Identify the Critical Angle
The critical angle C can be defined as:
C=sin−1(n1n2)
For maximum lateral shift, we want I to approach 90 degrees, which means that R approaches the critical angle.
Step 6: Conclusion
Thus, the angle of incidence I for which the lateral shift is maximum is:
I=90∘
Final Answer
The angle of incidence at which the lateral shift produced by a parallel-sided glass plate is maximum is 90∘.
---
Lateral shift (S) is defined as the horizontal displacement of a light ray as it passes through a parallel-sided glass plate. It can be calculated using the formula:
- t = thickness of the glass plate
- I = angle of incidence
- R = angle of refraction
To maximize the lateral shift S, we need to maximize both secR and sin(I−R).
According to Snell's Law:
The angle of refraction R will be maximum when the angle of incidence I is also maximized. The maximum angle of incidence occurs when the light ray is incident parallel to the surface of the glass plate, which corresponds to the critical angle condition.
The critical angle C can be defined as:
Thus, the angle of incidence I for which the lateral shift is maximum is:
The angle of incidence at which the lateral shift produced by a parallel-sided glass plate is maximum is 90∘.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Revision Exercises (Fill in the Blanks)10videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Revision Exercises (Short Answer Questions)43videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Revision Exercises (Very Short Answer Questions)82videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION15videos
NUCLEI
- BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION12videos
SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS
Similar Questions
Knowledge Check
- Question 1 - Select One
The lateral shift produced due to parallel sided glass slab depends on
Aangle of incidenceBthickness of the glass slabCthe refarctive index of the material of the slabDall of these - Question 2 - Select One
A ray of light is incident on the surface of a glass plate of thickness t. I fthe angle of incidence θ is small, the emerging ray would be displaced side ways by an amount
[Taken = refractive index of glass)Atθn/(n+1)Btθ(n−1)/nCtθn/(n−1)Dtθ(n+1)/n - Question 3 - Select One
In the experiment to trace the path of a ray of light through a parallel sided glass slab, a student measured the angles of refraction for three different angles of incidence. He will find that :
Aangle of refraction is always equal to the angle of incidenceBangle of refraction is always smaller than the angle of incidenceCangle of refraction is always greater than the angle of incidenceDangle of refraction can be smaller or greater than the angle of incidence depending on the refractive index of glass slab
A glass plate has a thickness t and refravtive index μ A light ray is allowed to incident in the plate from air. Find at what angle of incidence will the rays refracted and reflected by the plate be perpendicular to each other ? For this angle of incidence, calculate the lateral displacement of the ray
t(μ2−1)μ√1+μ2View SolutionA beam of light is converging towards a certain point. A parallel sided glass plate is introduced in the path of the converging beam. How will the point of convergence be shifted ?
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?View Solution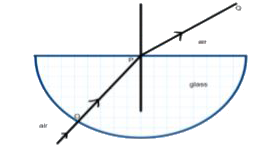
The angle of incidence from air to glass at the point O on the hemispherical glass slab is.View Solution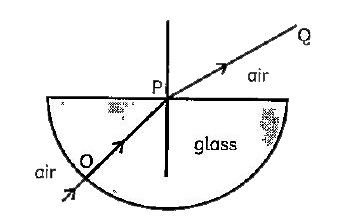
The angle of incidence from air to glass at the point O on the hemispherical glass slab is.View Solution

