Deduce the equivalent focal length of two convex lenses of focal lengths F1andF2 when placed in contact.
To deduce the equivalent focal length of two convex lenses with focal lengths F1 and F2 when placed in contact, we can follow these steps:
1. Understanding Lens Power:
The power P of a lens is defined as the reciprocal of its focal length f:
P=1f
Therefore, for two lenses with focal lengths F1 and F2, their powers are:
P1=1F1andP2=1F2
2. Total Power of the System:
When two lenses are placed in contact, the total power Pnet of the system is the sum of the individual powers:
Pnet=P1+P2
3. Substituting the Powers:
Substitute the expressions for P1 and P2 into the equation for total power:
Pnet=1F1+1F2
4. Finding the Equivalent Focal Length:
The equivalent focal length Fequiv is related to the total power by:
Pnet=1Fequiv
Therefore, we can set up the equation:
1Fequiv=1F1+1F2
5. Combining the Fractions:
To combine the fractions on the right-hand side, we find a common denominator:
1Fequiv=F2+F1F1F2
6. Inverting to Find Fequiv:
To find Fequiv, we take the reciprocal of both sides:
Fequiv=F1F2F1+F2
Final Result:
Thus, the equivalent focal length of two convex lenses placed in contact is given by:
Fequiv=F1F2F1+F2
The power P of a lens is defined as the reciprocal of its focal length f:
P=1f
Therefore, for two lenses with focal lengths F1 and F2, their powers are:
P1=1F1andP2=1F2
When two lenses are placed in contact, the total power Pnet of the system is the sum of the individual powers:
Pnet=P1+P2
Substitute the expressions for P1 and P2 into the equation for total power:
Pnet=1F1+1F2
The equivalent focal length Fequiv is related to the total power by:
Pnet=1Fequiv
Therefore, we can set up the equation:
1Fequiv=1F1+1F2
To combine the fractions on the right-hand side, we find a common denominator:
1Fequiv=F2+F1F1F2
To find Fequiv, we take the reciprocal of both sides:
Fequiv=F1F2F1+F2
Thus, the equivalent focal length of two convex lenses placed in contact is given by:
Fequiv=F1F2F1+F2
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Revision Exercises (Long Answer Questions)
20 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Revision Exercises (Numerical Problems)
36 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Revision Exercises (Fill in the Blanks)
10 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
12 Videos
Similar Questions
A thin convex lens has focal length f1 and a concave lens has focal length f2. They are kept in contact. Now, match the following two columns.

View SolutionDerive the relation : 1F=1f1+1f2,where f1 and f2 are focal length of two thin lenses and F is the focal length of the combination in contact.
View Solution
Knowledge Check
Arrange the following combinations in the increasing order of focal length
Two piano convex lenses of focal lengths 15 cm and 30 cm in contact
Two convex lens of focal lengths 40 cm and 50 cm in contact
Two convex lenses of focal length 20 cm separated by 5 cmAa, b, cBb, a, cCa, c, bDc, a, bArrange the following combinations in the increasing order of focal length
a) Two piano convex lenses of focal lengths 20 cm and 30 cm in contact
b) Two convex lens of focal lengths 20 cm and 10 cm in contact
Two convex lenses of focal length 25 cm separated by 5 cm.Aa, b, cBb, a, cCa, c, bDc, b, aA convex lens of focal length 40 cm a concave lens of focal length 40 and a concave lens of focal length 15 cm are placed in contact. The power of this combination of are placed in contact. The power of this combination in diopters is
A+1.5B−1.5C+6.67D−6.67
(a) Using the ray diagram for a system of two lenses of focal lengths f1andf2 in contact with each other, show that the two lens system can be regarded as equivalent to a single lens of focal length f, where
1f=1f1+1f2
Also write the relation for the equivalent power of the lens combination.
(b) Determine the position of the image formed by the lens combination given in the figure.
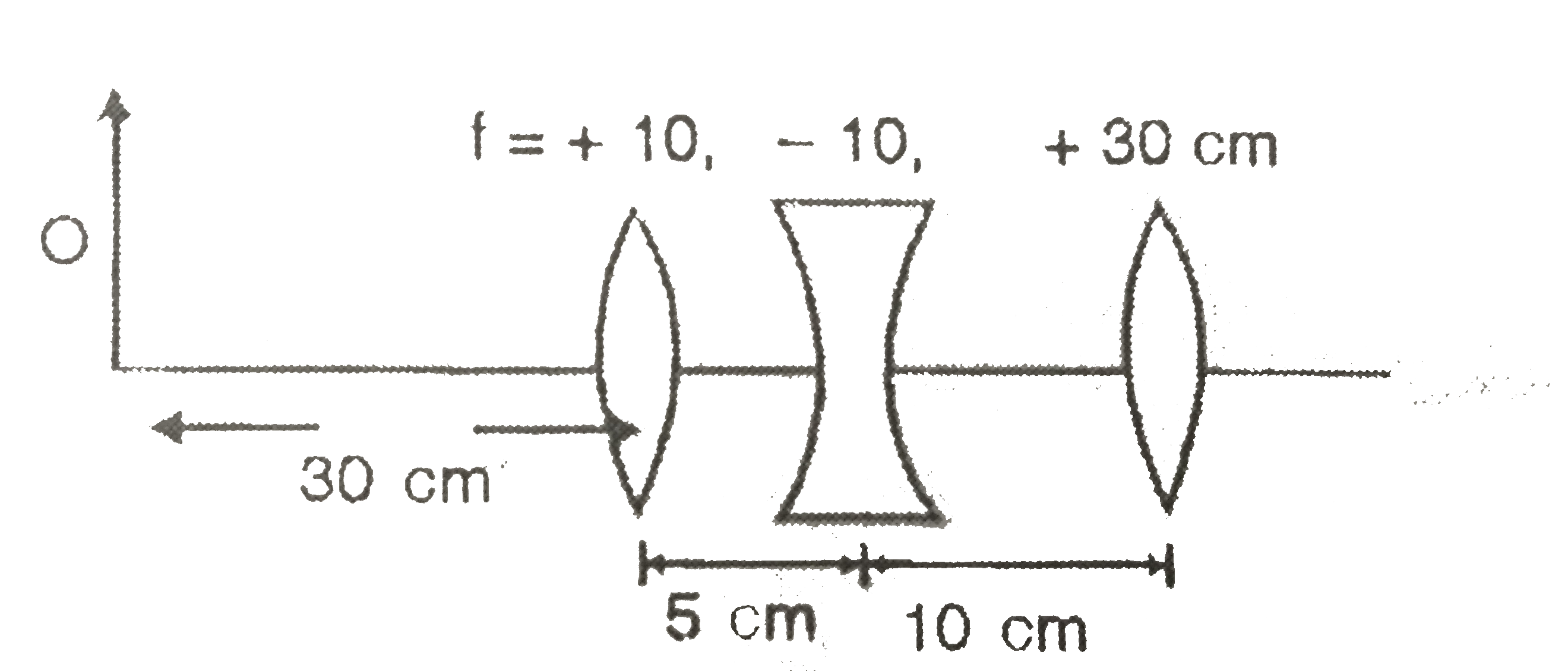
View SolutionWe combined a convex lens of focal length f1 and concave lens of focal lengths f2 and their combined focal length was F . The combination of these lenses will behave like a concave lens, if
View SolutionA convex lens of focal length x and a concave lens of focal length y are placed in contact. The focal length of the combination is
View SolutionA convex lens of focal length A and a concave lens of focal length B are placed in contact. The focal length of the combination is
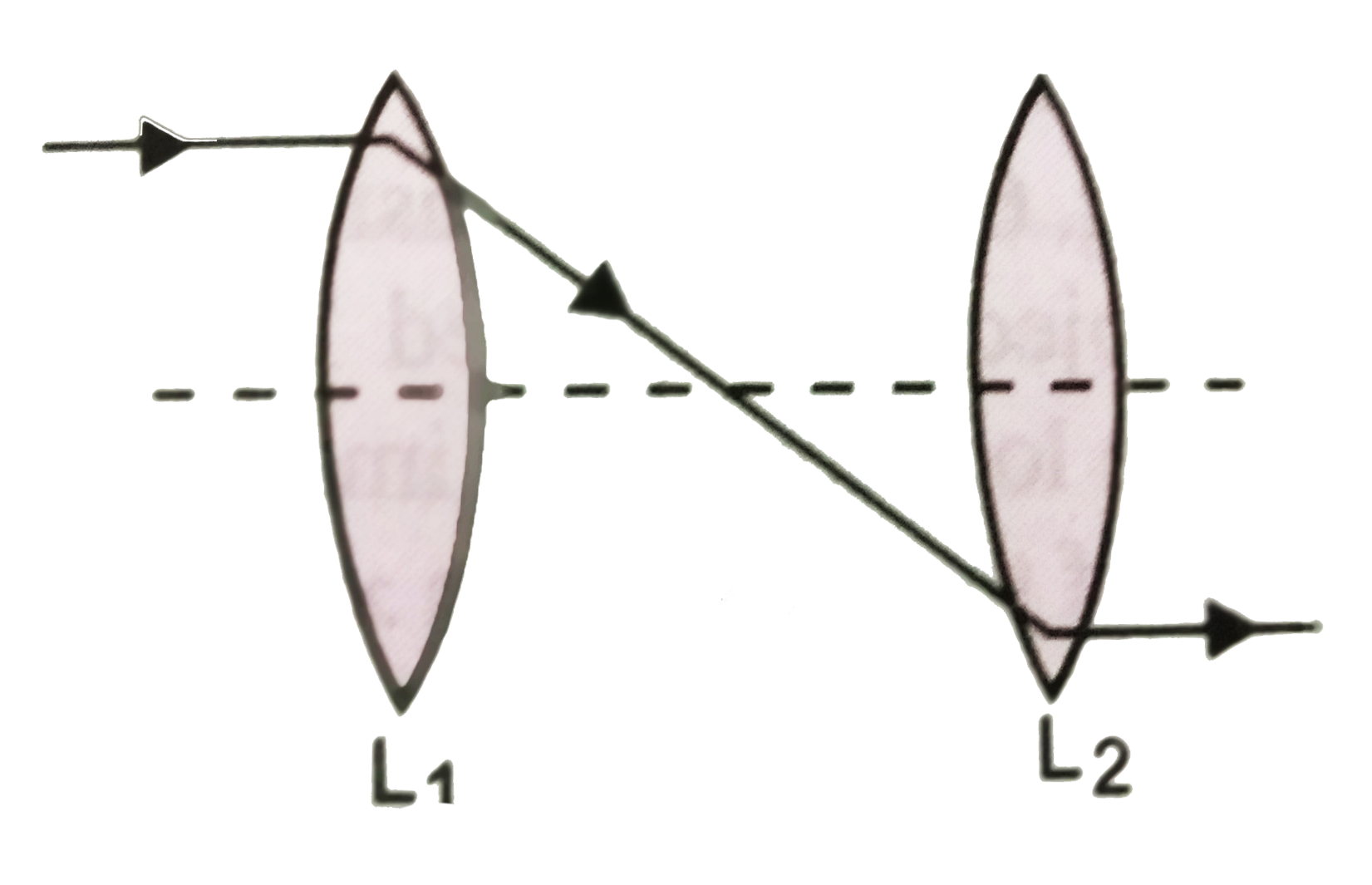
View SolutionIn Fig., there are two convex lenses L1 and L2 having focal lengths F1 and F2 respectively. The distance between L1 and L2 will be :
View Solution
