R is the radius of curvature for both the surfaces of lens shown in figure. Refractive index μ1,μ2andμ3 are indicated in the figure. Light rays are incident from the side of refractive index μ1 as shown. If f is focal length of lens then find f/R for μ1=1,μ2=1.5,μ3=2.
|0123456789|
The correct Answer is:2
To find the relationship between the focal length f and the radius of curvature R for the given lens using the Lensmaker's formula, we can follow these steps:
Step 1: Apply the Lensmaker's Formula for Surface 1
For the first surface of the lens, we can use the Lensmaker's formula:
μ2v1−μ1u1=μ2−μ1R
Where:
- μ1=1 (refractive index of the medium from which light is coming)
- μ2=1.5 (refractive index of the lens)
- u1=−∞ (object distance for parallel rays)
- v1 is the image distance from surface 1.
Since u1 is very large (for parallel rays), we can approximate:
μ2v1=μ2−μ1R
Rearranging gives us:
v1=μ2Rμ2−μ1
Substituting the values:
v1=1.5R1.5−1=1.5R0.5=3R
Step 2: Apply the Lensmaker's Formula for Surface 2
Now, we apply the Lensmaker's formula for the second surface:
μ3v2−μ2v1=μ3−μ2R
Where:
- μ3=2 (refractive index of the medium on the other side of the lens)
- v2 is the final image distance from surface 2.
Substituting v1=3R:
2v2−1.53R=2−1.5R
This simplifies to:
2v2−0.53R=0.5R
Step 3: Solve for v2
Rearranging gives us:
2v2=0.5R+0.53R
Finding a common denominator for the right side:
2v2=0.5⋅3+0.53R=1.53R=0.5R
Thus:
2v2=0.5R
Cross-multiplying gives:
2R=0.5v2⟹v2=2R0.5=4R
Step 4: Relate f to R
Since v2 is the focal length f:
f=4R
Step 5: Find fR
Now, we can find fR:
fR=4RR=4
Final Answer:
Thus, the value of fR is 4.
---
For the first surface of the lens, we can use the Lensmaker's formula:
- μ1=1 (refractive index of the medium from which light is coming)
- μ2=1.5 (refractive index of the lens)
- u1=−∞ (object distance for parallel rays)
- v1 is the image distance from surface 1.
Now, we apply the Lensmaker's formula for the second surface:
- μ3=2 (refractive index of the medium on the other side of the lens)
- v2 is the final image distance from surface 2.
Rearranging gives us:
Since v2 is the focal length f:
Now, we can find fR:
Thus, the value of fR is 4.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - CHAPTER PRACTICE TEST14videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - OBJECTIVE TYPE QUESTIONS (MATRIX MATCH TYPE QUESTIONS)1videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION15videos
NUCLEI
- BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION12videos
SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS
Similar Questions
What is the relation between the refractive indicesμ,μ1 and μ2 if the behaviour of light rays is shown in Figure.
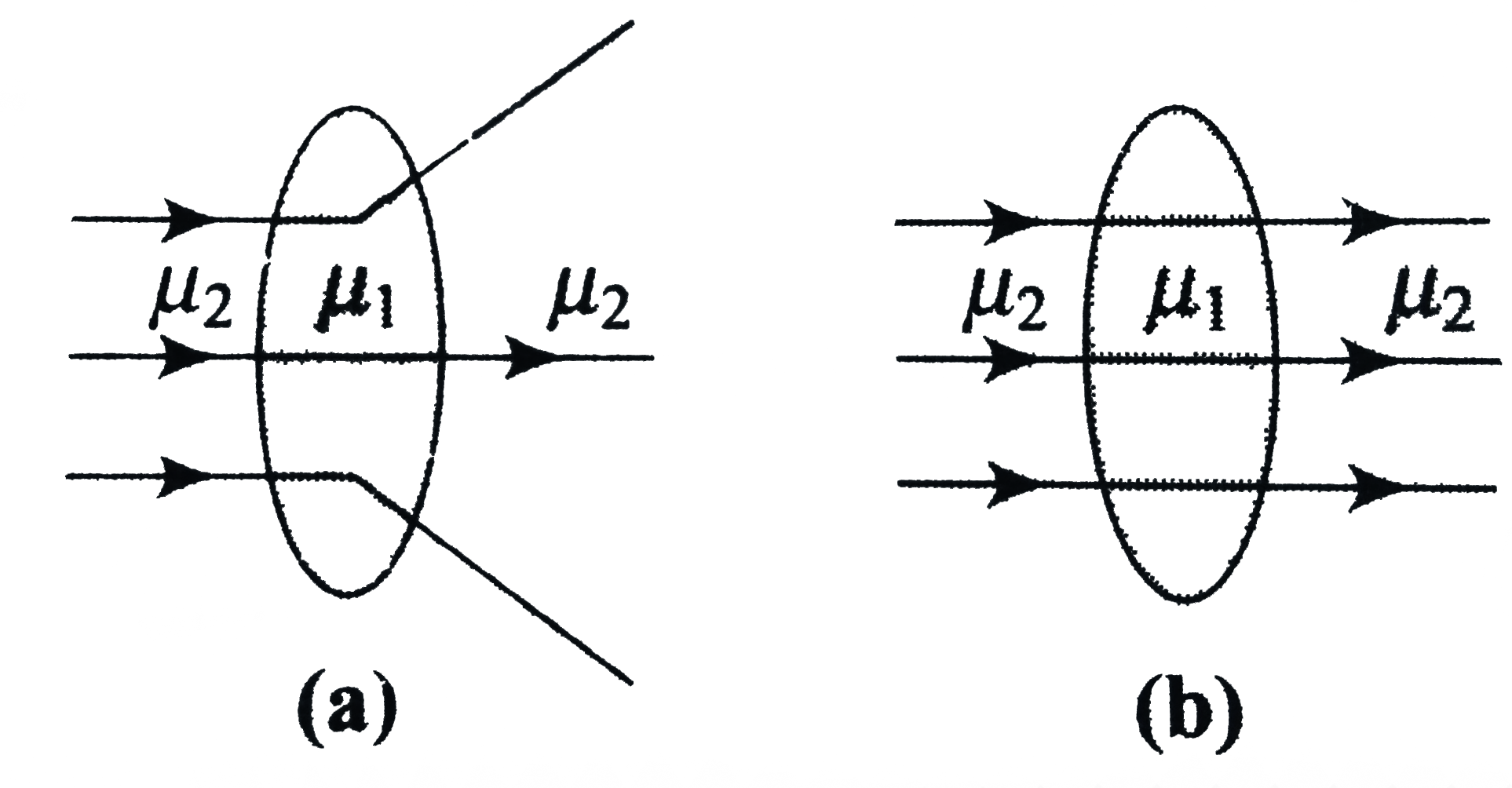 View Solution
View SolutionA thin lens made of a material of refractive index μ0 has a focal length f0 in air. Find the focal length of this lens if it is immersed in a liquid of refractive index μ.
View Solution
Knowledge Check
- Question 1 - Select One
If the behaviour of light rays is as shown in the figure. The relation between refractive indices μ,μ1 "and" μ2 is
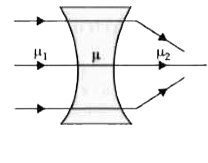 Aμ>μ2>μ1Bμ<μ2<μ1Cμ<μ2,μ=μ1Dμ2<μ1,μ=μ2
Aμ>μ2>μ1Bμ<μ2<μ1Cμ<μ2,μ=μ1Dμ2<μ1,μ=μ2 - Question 2 - Select One
The relation between refractive indices u,μ1,μ2. if the behaviour of light ray is as shown in figure
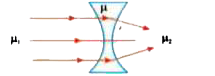 Aμ>μ1>μ2Bμ<μ2<μ1Cμ<μ2,μ=μ1Dμ2<μ1,μ=μ2
Aμ>μ1>μ2Bμ<μ2<μ1Cμ<μ2,μ=μ1Dμ2<μ1,μ=μ2 - Question 3 - Select One
A bi-convex lens is cut from the middle as shown in figure. Refractive index of material of lens is 32. Now lens-1 (as shown in figure) is immersed in a liquid of refractive index μ0. By doing so it is observed that its focal length becomes equal to lens-2. What is the value of μ0 ?
 A1.3B1.1C1.4D1.2
A1.3B1.1C1.4D1.2
An equiconvex lens of refractive index μ2 is placed such that the refractive :
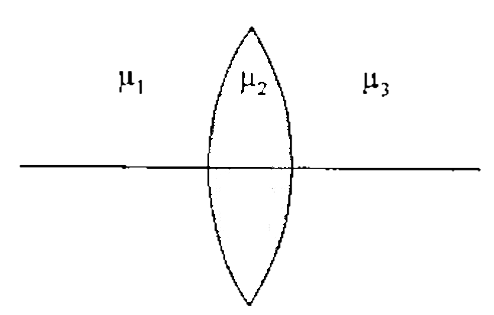 View Solution
View SolutionFrom the figure shown establish a relation between μ1,μ2,μ3.
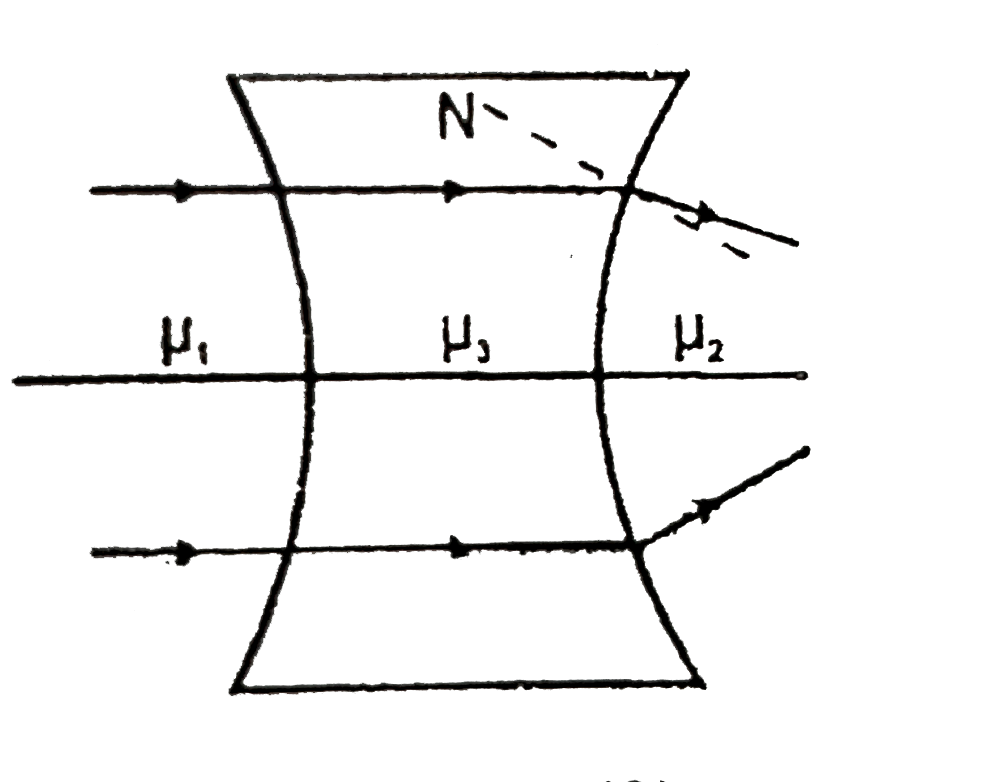 View Solution
View SolutionIf the plane surface of a plano-convex lens of radius of curvature R and refractive index μ is silvered, then its focal length would be
View SolutionA convex lens made up of material of refractive index μ1, is immersed in a medium of refractive index μ2 as shown in the figure. The relation between μ1 and μ2 is
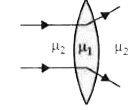 View Solution
View SolutionA lens made of material of Refractive index μ2 is surrounded by a medium of Refractive Index μ1. The focal length f is related as
View Solution

