सिद्ध कीजिए कि बिन्दु (1,1), (-2,7) और (3 -3) सरेख है।
Step by step video & image solution for सिद्ध कीजिए कि बिन्दु (1,1), (-2,7) और (3 -3) सरेख है। by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - SCIENCE PUBLICATIONCHAPTER - अभ्यास हेतु सभी अध्यायों के मह्त्वपूर्ण अभ्यास प्रश्न EXERCISE - बिन्दुपथ (Locus)6videos
अभ्यास हेतु सभी अध्यायों के मह्त्वपूर्ण अभ्यास प्रश्न
- BOOK - SCIENCE PUBLICATIONCHAPTER - अभ्यास हेतु सभी अध्यायों के मह्त्वपूर्ण अभ्यास प्रश्न EXERCISE - समरूपता (Similarity)11videos
अभ्यास हेतु सभी अध्यायों के मह्त्वपूर्ण अभ्यास प्रश्न
- BOOK - SCIENCE PUBLICATIONCHAPTER - अभ्यास हेतु सभी अध्यायों के मह्त्वपूर्ण अभ्यास प्रश्न EXERCISE - ऊँचाई और दूरी (Height and Distance)8videos
अभ्यास हेतु सभी अध्यायों के मह्त्वपूर्ण अभ्यास प्रश्न
- BOOK - SCIENCE PUBLICATIONCHAPTER - ऊँचाई और दुरी EXERCISE - अन्य महत्वपूर्ण प्रश्न5videos
ऊँचाई और दुरी
Similar Questions
त्रिभुज के तीनों शीर्ष लम्ब संगामी होते हैं तो उस संगमन बिन्दु को कहते है।
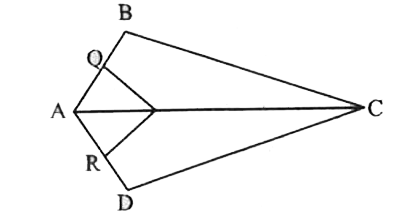
03:53View Solutionचित्र में PQ || BC तथा PR || CD हो तो सिद्ध कीजिए कि
ARAD=AQAB
 03:12View Solution
03:12View Solutionएक मीनार केआधार से और एक सरल रेखा में 4 मीटर और 9 मीटर की दूरी पर स्थित दो बिन्दुओं से मीनार के शिखर को उन्नयन कोण? एक पूरक कोण है। सिद्ध कीजिए कि मीनार की ऊँचाई 6 मीटर है।
03:54View Solution50 मीटर ऊँचे पुल से किसी नाव का अवनमन कोण 30∘ है। नाव की पुल से क्षैतिज दूरी ज्ञात कीजिए।
02:50View Solutionसिद्ध कीजिए कि रेखाएँ x+32=y+53=z−7−3 और x+14=y+15=z+1−1 समतलीय है।
03:34View Solutionसिद्ध कीजिए कि निम्नलिखित संख्याएँ अपरिमेय संख्याएँ है-
32√503:33View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
03:51View Solutionयदि दो सदिश ¯a और ¯b इस प्रकार हैं कि ∣∣¯a+¯b∣∣=∣∣¯b∣∣, तब सिद्ध कीजिए कि ¯a+2¯b, सदिश ¯a पर लम्ब है |
06:18View Solutionयदि z=3−5i,तो सिद्ध कीजिए कि :
z3−10z2+58z−136=006:40View Solutionसिद्ध कीजिए कि सम्मिश्र संख्याओं 0, 2i और √3+i को निरूपित करने वाले बिंदु समबाहु त्रिभुज के शीर्ष है।
02:09View Solutionसिद्ध कीजिए कि किसी गुणोत्तर श्रेढ़ी के आरम्भ और अंत से संदुररस्थ पदों का गुणनफलन सदैव अचर रहता है ।
02:51View Solutionयदि बिन्दु (a,b),(a',b') और (a−a',b−b') संरेख हो तो सिद्ध कीजिए कि
ab'=a'b.
साथ ही यह भी सिद्ध कीजिए कि इन बिन्दुओं से होकर जाने वाली रेखा मुलबिन्दु से होकर जाती है।02:56View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
02:19View Solutionयदि f:R→R इस प्रकार है कि f(x) = |x|, तो सिद्ध कीजिए कि fof = f .
04:47View Solutionसिद्ध कीजिए कि f(x)=ax,o<a<1,R में ह्रासमान है।
02:56View Solutionसिद्ध कीजिए कि फलन सम्मुख दिए गए अन्तराल में ह्रासमान है ।
f(x)=x2−2x+3,x<103:43View Solution

