एक पात्र की पेंदी ,4.0 cm मोटी काँच (μ=1.5) की स्लैब है। पात्र में क्रमशः 6.0 cm और 8.0 cm गहराई वाले दो अमिश्रणीय द्रव A और B हैं। पात्र में से देखें जाने पर काँच के स्लैब की पेंदी के ऊपरी पृष्ठ पर निशान की आभासी स्थिति क्या है ? A और B के अपवर्तनांक क्रमशः 1.4 और 1.3 हैं।
हमें पता है कि μ=dRdA या dA=dRμ
और हमें यह भी पता है कि (dR)काँच=4cm,
(dR)A=6cm,(dR)B=8cm,aμg=1.5,aμA=1.4 और aμB=1.3
प्रत्येक माध्यम के कारण निशान का विस्थापन
d=dR−dA
या
d=dR−dRμ=dR[1−1μ]=dR(μ−1μ)
तीनों माध्यमों के कारण निशान का कुल विस्थापन
=d1+d2+d3
=(dR)काँच[aμg−1aμg]+(dR)A[aμA−1aμA]+(dR)B[aμB−1aμB]
=(4cm)(1.5−11.5)+(6cm)(1.4−11.4)+(8cm))(1.3−11.3)
=(4×0.51.5+6×0.41.4+8×0.31.3)cm
=(1.33+1.71+18.5)cm=4.89cm
निशान की आभासी स्थिति =18−4.89=13.11cm∗
Topper's Solved these Questions
- समतल पृष्ठों पर अपवर्तनBOOK - GRB PUBLICATION HINDICHAPTER - समतल पृष्ठों पर अपवर्तनEXERCISE - प्रश्नोत्तरी(उच्चस्तरीय चिंतन )
28 Videos
- समतल पृष्ठों पर अपवर्तनBOOK - GRB PUBLICATION HINDICHAPTER - समतल पृष्ठों पर अपवर्तनEXERCISE - प्रश्नोत्तरी 1 अंक
22 Videos
- समतल पृष्ठों पर अपवर्तनBOOK - GRB PUBLICATION HINDICHAPTER - समतल पृष्ठों पर अपवर्तनEXERCISE - विषय -आधारति अभ्यास
35 Videos
- समतल और गोलीय पृष्ठों पर परावर्तन BOOK - GRB PUBLICATION HINDICHAPTER - समतल और गोलीय पृष्ठों पर परावर्तन EXERCISE - अभ्यास
14 Videos
Similar Questions
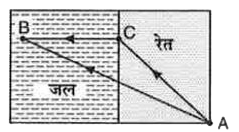
बिंदु B पर चित्र एक तैराक को सहयता चाहिए। बिंदु A पर स्थित दो अलग-अलग जीवनरक्षक(lifeguards) अपने मीनार से एक ही साथ निकलते हैं परन्तु अलग -अलग मार्ग पकड़ते हैं। यद्यपि दोनों जीवनरक्षक रेत पर एक ही चाल से दौड़ते हैं और जल में एक ही चाल से तैरते हैं,फिर भी लम्बा मार्ग (ACB ) पकड़ने वाला जीवनरक्षक,A से B तक छोटा सीधा मार्ग पकड़ने वाले जीवनरक्षक से पहले बिंदु B पर पहले पहुँचता है। व्याख्या करें।
View Solutionएक ही आवृत्ति वाला प्रकाश का स्त्रोत, मछली के टैंक में जल में डुबाया जाता है| बीम, जल में टैंक के पार्श्व पर दोहरे कांच के शीशों में से ( हर काँच के शीशे का μ अलग-अलग है ) और वायु में चलती है। आम तौर पर प्रकाश के (a) आवृत्ति और (b) तरंगदैध्य्र को क्या होता है जब यह बाहर हवा में निकलती है ?
View Solutionकाँच का अपवर्तनांक 1.5 और जल का 1.3 है। यदि जल में प्रकाश की चाल 2.25×108m/s, हो, तो काँच में प्रकाश की चाल क्या है ?
View Solutionकिसी कमरे की दीवार पर लगे समतल दर्पण का न्यूनतम साइज़ निकालें जिससे कमरे के बीचों - बीच खड़ा कोई व्यक्ति अपने पीछे की दीवार का पूरा प्रतिबिम्ब देख सके।
View Solutionघूर्णन द्रव प्रश्न पात्र की दीवारों पर द्रव द्वारा बल
View SolutionTwo circles of radii 7 cm and 9 cm intersect at the points A and B. If AB=6cm, and the distance between the centres of the circles is x cm, then the value of x (to the closest integer) is: 7 cm और 9 cm त्रिज्या के दो वृत्त, बिंदु A और B पर एक दूसरे को काटते हैं| अगर AB=6 cm है, और वृत्त के केंद्रों के बीच की दूरी x cm है तो x का मान (निकटतमें पूर्णाक में) है:
View Solutionअभिक्रिया a+bhArrc+d के लिए प्रार में a और b की सांद्रताएं समान होती है। और साम्यावस्था पर d की सांद्रता a की सांद्रता से दोगुनी होती है। अभिक्रिया के लिए साम्य स्थिरांक क्या होगा?
View Solutionएक आदर्श गैस के दस मोलों को एक बंद पात्र में भरा जाता है । पात्र में बेलन और पिस्टन के प्रकार की व्यवस्था है और 0.821 atm पर गैस का दाब स्थिर रहता है। निम्नलिखित में से कौन सा आलेख logV और logT के परिवर्तन का सही निरूपण करता है? (V= आयतन(लीटर में) और T= ताप (केलिवन में)
View SolutionNO_2 और N_2O_4 नाइट्रोजन डाइऑक्साइड के दो रूप हैं। एक गैसीय अवस्था में मौजूद होता है जबकि दूसरा द्रव अवस्था में। NO_2 और N_2O_4 रूपों की प्रकृति है:
View Solutionनिम्नलिखित यौगिक के जल अपघटित उत्पादों में से एक, काँच पात्र की सिलिका के साथ अभिक्रिया नहीं करता है?
View Solution2-पेन्टाइन में HBr के 1 मोल के योग से निर्मित एक ब्रोमो यौगिक के संभावित संरचनात्मक और संरूपण समावयवियों की संख्या क्रमशः है
View Solutionएक यौगिक AB में, A और B के बीच विद्युत् ऋणता का अंतर 1.9 है। A और B की परमाणु त्रिज्या 4Å और 2Å हैं। A और B परमाणुओं के बीच की दूरी अर्थात dA−B है
View Solutionबोरिक अम्ल में बोरॉन और ऑक्सीजन परमाणुओं के संकरण की अवस्था क्रमशः हैं:
View Solutionजब AX और BX2 के जलीय विलयन के माध्यम से विद्युत् के कूलॉम की बराबर संख्या प्रवाहित की जाती है और यदि A और B के निक्षेपित मोलों की संख्या क्रमशः Y और Z है तब-
View Solutionनिम्नलिखित में से प्रशांतक और शामक के रूप में उपयोग की जाने वाली औषधियाँ हैं:
View SolutionCr और Fe की परमाणु संख्या क्रमशः 24 और 26 हैं, निम्नलिखित में से कौन इलेक्ट्रॉन के प्रचक्रण के साथ अनुचुम्बकीय है?
View Solution
