A: बामर श्रैणी, वैधुतचुम्बकीय स्पेक्ट्रम के दृश्य क्षेन्न में पड़ती है ।
R: 1λ=R[122−1n2] जहाँ n=3,4,5
A और R दोनों सत्य हैं और R , A की सही व्याख्या हैं।
A और R दोनों सत्य हैं परन्तु R , A की सही व्याख्या नहीं हैं।
A सत्य है परन्तु R असत्य हैं।
A और R दोनों असत्य हैं।
The correct Answer is:B
जब, n = 3 तो λ=6563Å और जब n=∞ तो λ=3646Å
(दृश्य क्षेत्र 3900Å से 7800Å तक है )
Topper's Solved these Questions
- BOOK - GRB PUBLICATION HINDICHAPTER - नाभिक EXERCISE - प्रतियोगिता सामग्री (पूर्णांक उत्तर वाले प्रश्न )7videos
नाभिक
- BOOK - GRB PUBLICATION HINDICHAPTER - नाभिक EXERCISE - प्रतियोगिता सामग्री (सत्य या असत्य )31videos
नाभिक
- BOOK - GRB PUBLICATION HINDICHAPTER - नाभिक EXERCISE - प्रतियोगिता सामग्री (कॉलम मिलाना)7videos
नाभिक
- BOOK - GRB PUBLICATION HINDICHAPTER - धारिता और परावैधुत पदार्थ EXERCISE - प्रतियोगिता समाग्री (बहुविकल्पीय प्रश्न : एक या एक से अधिक सही विकल्प (रिक्त स्थान भरना )15videos
धारिता और परावैधुत पदार्थ
- BOOK - GRB PUBLICATION HINDICHAPTER - परमाणुEXERCISE - NCERT पाठ्यपुस्तक अभ्यास उत्तरो सहित16videos
परमाणु
Similar Questions
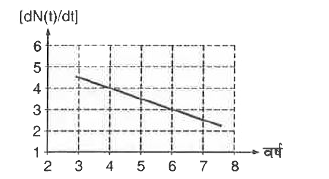
किसी रेडियोसक्रिय तत्व की अर्ध - आयु निकालने के लिए एक छात्र ln|dN(t)/dt| का एक t साथ ग्राफ़ बनता है [चित्र] यहाँ dN(t)/dt,t समय पर रेडियोसक्रिय क्षय की दर है। यदि इस तत्व के रेडियोसक्रिय नाभिकों की संख्या , 4.16 वर्षों के बाद p के घटक से कम हो जाती हो , तो p का मान है।
 06:28View Solution
06:28View Solutionकिसी परमाणु में इलेक्ट्रॉन की कुल ऊर्जा धनात्मक होती है ।
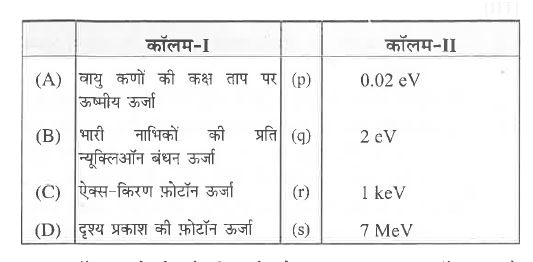
03:53View Solutionकॉलम - I की सूची में दी गई भौतिक राशियों को कॉलम - II की सूची में यादृच्छिक रूप से दिए गए उनके मानों के साथ मिलाएँ।
 03:15View Solution
03:15View Solutionएकसमान धनात्मक आवेश Q (कूलॉम) वाली दो छोटी गेंदे एक स्टैण्ड से जुडी एक हुक के साथ L (मीटर ) लम्बी दो विधुतरोधी डोरियों से लटकाई जाती है। यह समूह उपग्रह द्वारा अंतरिक्ष में ले जाय जाता है जहाँ कोई गुरुत्व नहीं (भारहीनता की स्थिति ) है। दोनों डोरियों के बीच कोण .......... है और दोनों डोरियों में तनाव ........ न्यूटन है।
04:25View Solutionटॉमसन मॉडल में परमाणु का साइज रदरफोर्ड मॉडल में परमाण्विक साइज से है। (बहु ज्यादा/कोई अलग नहीं/काफी कम)
06:59View SolutionThe value of lim_(n rarr oo)(1*sum_(r=1)^(n)(r)+2*sum_(r=1)^(n-1)(r)+3sum_(r=1)^(n-2)(r)+....+n.1)/(n^(4))
07:46View SolutionIf Δr=∣∣ ∣ ∣∣1r2r2nn2nn(n1)22n+1∣∣ ∣ ∣∣, then the value of n∑r=1Δr is
06:12View SolutionIf Dr=∣∣ ∣ ∣∣r1n(n+1)22r−14n22r−152n−1∣∣ ∣ ∣∣, then the value of n∑r=1Dr, is
03:23View SolutionStatement -2: n∑r=0(−1)rnCrr+1=1n+1
Statement-2: n∑r=0(−1)rnCrr+1xr=1(n+1)x{1−(1−x)n+1}03:27View SolutionProve that :
(i) n!r!=n(n−1)(n−2)...(r+1)
(ii) (n−r+1)⋅n!(n−r+1)!=n!(n−r)!
(iii) n!r!(n−r)!+n!(r−1)!(n−r+1)!=(n+1)!r!(n−r+1)!11:45View Solutionसिद्ध कीजिए कि -
(i) .nPr.nPr−2=(n−r+1)(n−r+2)
(ii) .n−1Pr+r⋅.n−1Pr−1=.nPr
(iii).2nPn=2n⋅{1⋅3⋅5⋅…⋅(2n−1)}02:29View SolutionIf Cr stands for .nCr=n!r!n−r!andn∑r=1r.C2r=λ for n≥2, then λ is divisible by
03:09View Solution∣∣ ∣ ∣∣.n−1Cr−1.n−1Cr.n−1Cr+1.n−1Cr.n−1Cr+1.n−1Cr+2.nCr.nCr+1.nCr+2∣∣ ∣ ∣∣=
03:56View Solution2≤r≤n के लिए (nr)+2(nr−1)+(nr−2) =
04:50View SolutionLet for n∈N, f(n)=n∑r=0(−1)rCr2r+1(r+1)(r+2)
04:56View Solution

