Two point charges q1andq2, of magnitude +10−8Cand−10−8C, respectively, are placed 0.1 m apart. Calculate the electric fields at points A, B and C shown in figure.
The electric field vector E1A at A due to the positive charge q1, points towards the right and has a magnitude
E1A=(9×109)×10−8(0.05)2
=3.6×104NC−1
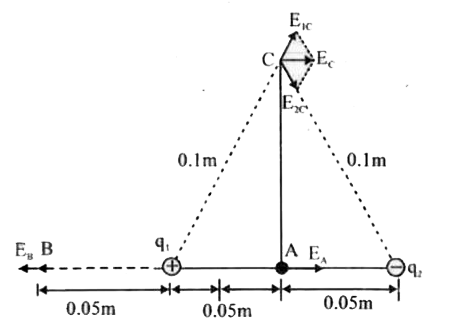
The electric field vector E2A at A due to the negative charge q2, points towards the right and has the same magnitude. Hence the magnitude of the total electric field EA at A is E1A+E2A=7.2×104NC−1.
EA is directed towards the right. The electric field vector E1B at B due to the positive charge q1, points towards the left and has a magnitude, E1B=(9×109)×10−8(0.05)2=3.6×102NC−1
The electric field vector E2B, at B due to the negative charge q2, points towards the right and has a magnitude E2B=(9×109)×(10−8)(0.15)2=4×103NC−1
The magnitude of the total electric field at B is EB=E1B−E2B=3.2×104NC−1EB is directed towards the left.
The magnitude of each electric field vector at point C, due to charge q1andq2 is
E1C=E2C=(9×109)×(10−8)(0.10)2=9×103NC−1
The directions in which these two vectors point are indicated in figure. The resultant of these two vectors is EC=E1cosπ3+E2cosπ3=9×103NC−1EC points towards the right.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - NEW JOYTHI PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Solution To Exercises From NCERT Text
26 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - NEW JOYTHI PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Evaluation Questions And Answers
12 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NEW JOYTHI PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - COMPETITIVE EXAM CORNER
15 Videos
- ELECTROMAGNETIC INDUCTION BOOK - NEW JOYTHI PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION EXERCISE - COMPETITIVE EXAM CORNER
13 Videos
Similar Questions
Two point charges q1andq2, of magnitude +10–8Cand–10–8C, respectively, are placed 0.1 m apart. Calculate the electric fields at points A, B and C shown in Fig. 1.14.
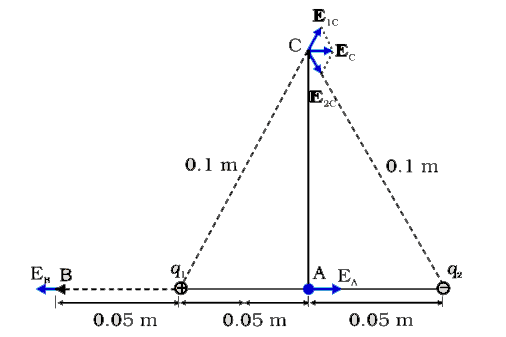
View SolutionTwo point charges q1andq2 of magnitude +10−8Cand−10−8C respectively are placed 0.1 m apart . Calculate the electric field at point B ,C and A
(##U_LIK_SP_PHY_XII_C01_E10_021_Q01.png" width="80%">
View Solution
Knowledge Check
Two point charges q1andq2, of magnitude +10–8Cand–10–8C, respectively, are placed 0.1 m apart. Calculate the electric fields at points A, B and C shown in Fig. 1.14.
 AEA=7.2×104NC−1 EB=3.2×104NC−1
AEA=7.2×104NC−1 EB=3.2×104NC−1
EB is directed towards the RIGHT.BEA=7.2×10−4NC−1 EB=3.2×104NC−1
EB is directed towards the left.CEA=7.2×104NC−1 EB=3.2×104NC−1
EB is directed towards the left.DEA=7.2×104NC−1 EB=3.2×10−4NC−1
EB is directed towards the left.Two point charges +10−7C and −10−7C are placed at A and B 20 cm apart as shown in the figure. Calculate the electric field at C, 20 cm apart from both A and B.
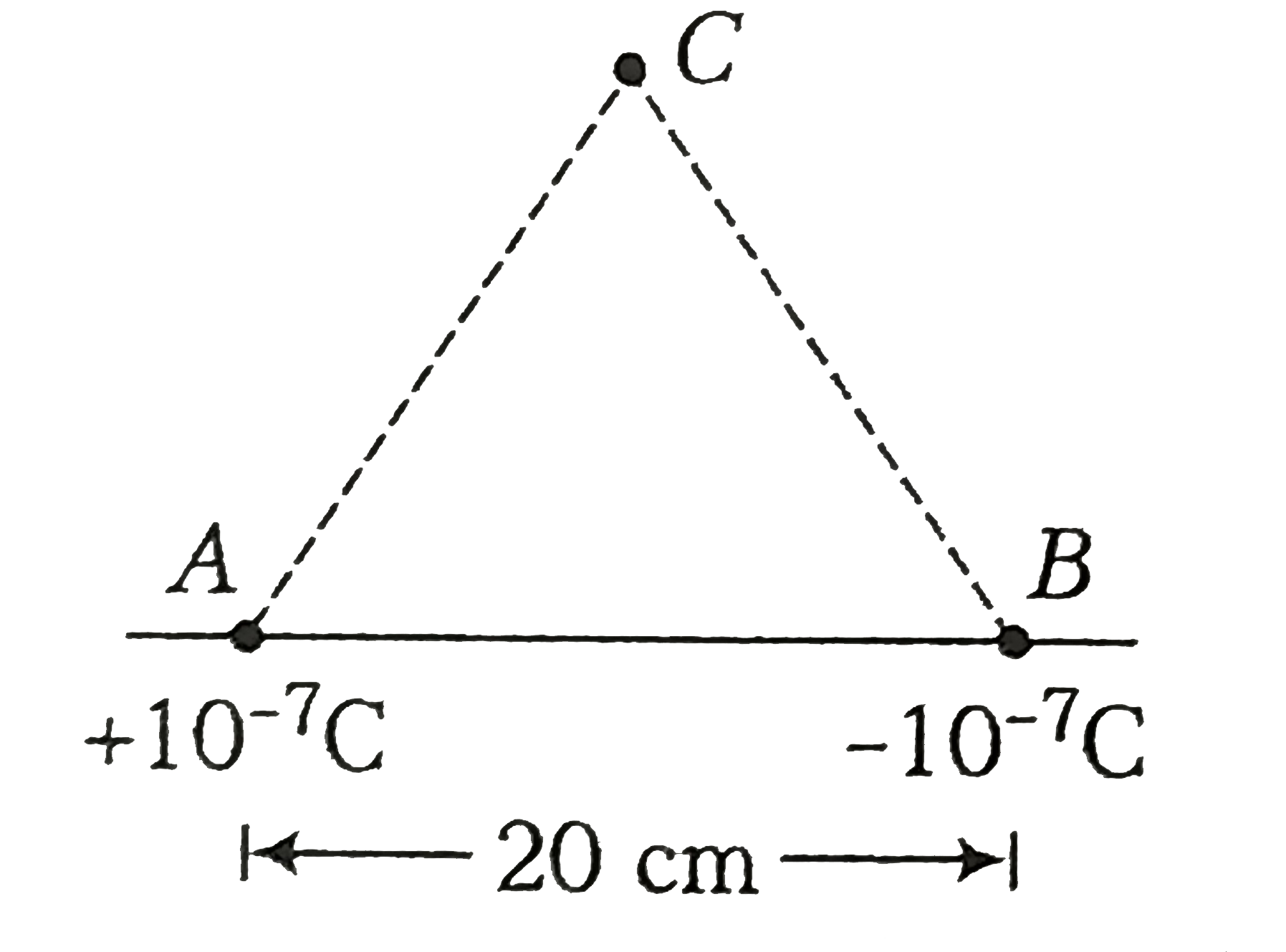 A1.5×10−5NC−1B2.2×104NC−1C3.5×106NC−1D3.0×105NC−1
A1.5×10−5NC−1B2.2×104NC−1C3.5×106NC−1D3.0×105NC−1
Two pont chargees q1 and q2 of 2×10−8C and −2×10−8C respectively are placed 0.4 m apart. Calculate the electric field at the centre of the line joining the two charges.
View SolutionTwo point charges q1andq2, of magnitude +10–8Cand–10–8C, respectively, are placed 0.1 m apart. Calculate the electric fields at points A, B and C shown in Fig. 1.14.

View SolutionTwo point charges +10−7C and −10−7C are placed at A and B 20 cm apart as shown in the figure. Calculate the electric field at C, 20 cm apart from both A and B.
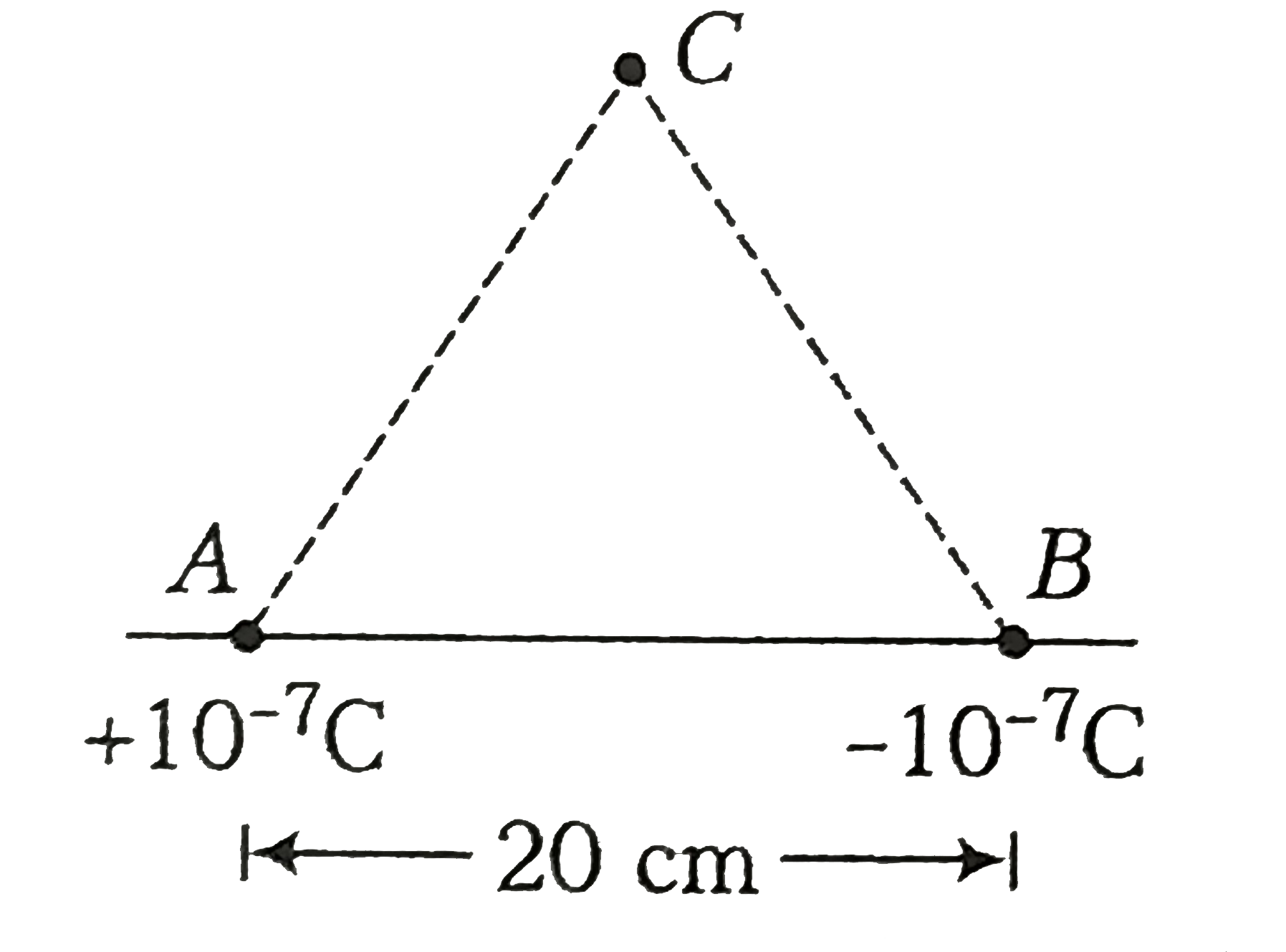
View SolutionTwo point charges, q1=10×10−8Candq2=−2×10−8C, are separated by a distance of 60 cm in air.
Also calculate the electrostatic potential energy of the system.
View SolutionTwo point charges of, 1 μC and -1 μC are kept at (-2 m, 0) and (2 m, 0) respectively. Calculate the electric field at point (0, 5 m).
View SolutionTwo point charges of magnitude 4 μC and-4μC are kept at points (-2 cm, 0) and (2 cm, 0) respectively. Calculate the magnitude of electric field intensity at points (0, 2 cm).
View Solution
