Two capacitors 3μFand6μF are first connected in series with a battery of emf 240V. The connection is broken and then connected in parallel. Find the final charges on the two capacitors.Solution in Tamil
The correct Answer is:160μC,320μC
Step by step video, text & image solution for Two capacitors 3muF and 6muF are first connected in series with a battery of emf 240V. The connection is broken and then connected in parallel. Find the final charges on the two capacitors. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - NEW JOYTHI PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Evaluation Questions And Answers41videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NEW JOYTHI PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Previous Year Questions2videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NEW JOYTHI PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Solution To Exercises From Ncert Texation36videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NEW JOYTHI PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - COMPETITIVE EXAM CORNER16videos
ELECTROMAGNETIC WAVES
- BOOK - NEW JOYTHI PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - COMPETITIVE EXAM CORNER13videos
MAGNETISM AND MATTER
Similar Questions
Fill up.
 02:32View Solution
02:32View SolutionA. A device to store electrical charge is called
a. Transformer
b. Capacitor
c. Resistor d. Inductor
B. What is meant by energy density of a parallel plate capacitor?
C. Derive an expression for the energy stored in a parallel plate capacitor.
D. What is the area of the plates of a 0.1μF parallel plate air capacitor, given that the separation between the plates is 0.1 mm.05:31View SolutionTwo charges 5×10−8Cand−3×10−8C are located 16 cm apart. At what point(s) on the line joining the two charges is the electric potential zero ? Take the potential at the infinity to be zero.
05:26View SolutionIf the total electromagnetic energy falling on a surface is U, then the total momentum delivered (for complete absorption) is
05:31View SolutionChoose the correct statement .
05:57View SolutionTwo capacitors C1=3μF and C2=6μF in series, are connected in parallel to a third capacitor C3=4μF. This arrangement is then connected to a battery of e.m.f., =30V, as shown. The energy lost by the battery in charging the capacitors
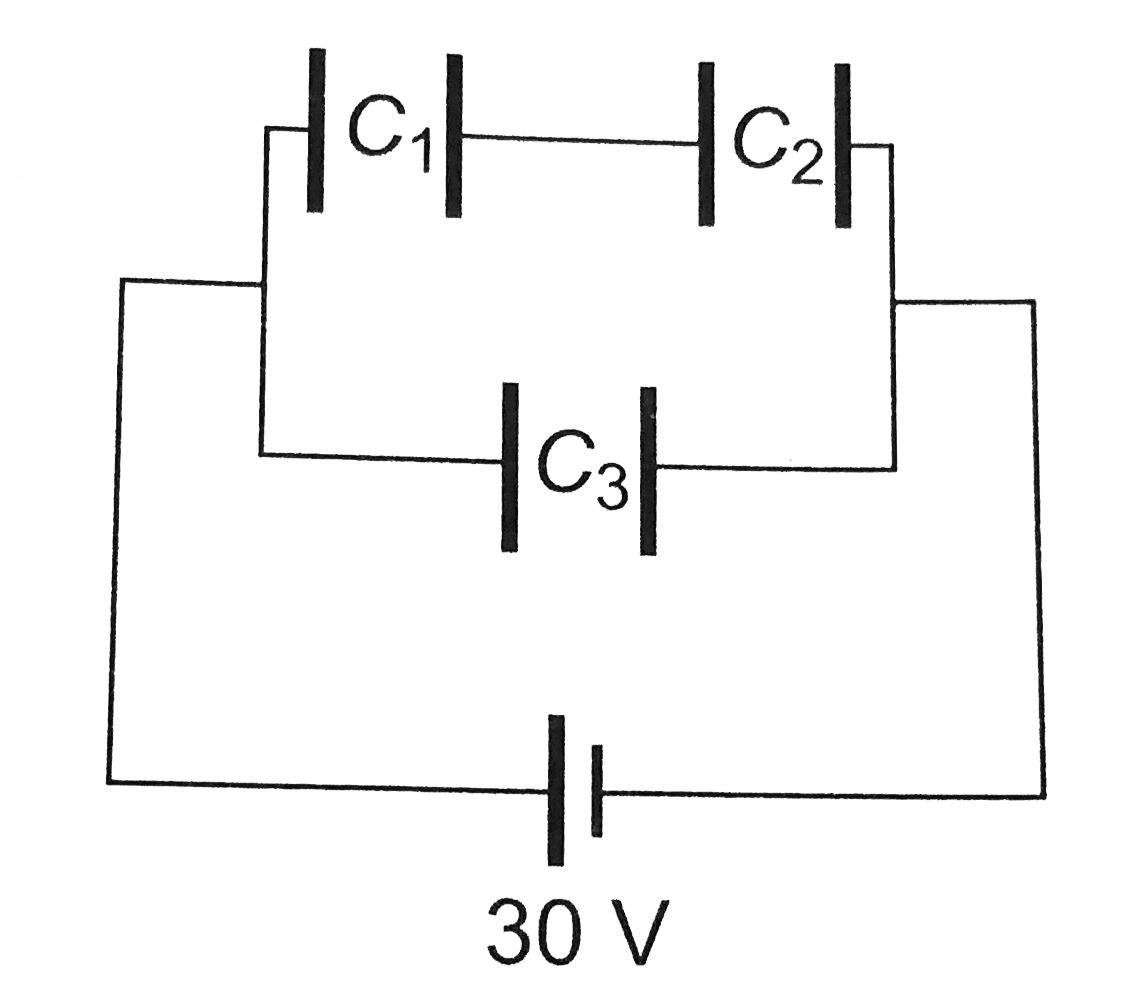 02:06View Solution
02:06View SolutionA 3μF and a 5μF capacitor are connected in series across a 30V battery. A 7μF capacitor is then connected in parallel across the 3μF capacitor. Choose the INCORRECT option :
02:50View SolutionTwo capacitors 3μF and 6μF are connected in series across a potential difference of 120V. Then the potential difference across 3μF capacitor is:
01:41View SolutionA 3μF and a 5μF capacitor are connected in series across a 30V battery. A 7μF capacitor is then connected in parallel across the 3μF capacitor. Choose the INCORRECT option :
04:12View SolutionTwo capacitors 2μF and 4μF are connected in parallel. A third capacitor of 6μFis connected in series. The combination is then connected across a 12V battery. The voltage across 2μF capacitor is:
05:09View SolutionThree capacitors of 3μF each are connected in series. This combination is connected in series to another combination of three capacitors of 1μF each in parallel. Find the total capacitance.
08:13View SolutionTwo capacitors of capacitances 4μF and 6μF are connected in series with a battery of 20 V. find the energy supplied by the battery.
03:08View SolutionTwo identical capacitors are first connected in series and then in parallel. The difference between their effective capacities is 3μF. The capacity of each capacitor is
02:41View SolutionThree capacitors, 3muF,6muF" and 6muF are connected in series to a source of 120V. The potential difference, in volts, across the 3muF capacitor will be
02:53View SolutionTwo capacitors of capacitances C_1 = 6muF and C_2 = 3muF are connected in series across a cell of emf 18 V. Calculate (i) the equivalent capacitance, (ii) the potential difference across each capacitor, (iii) the charge on each capacitor.
04:17View Solution

