Let the functions defined in Column I have domain (−π2,π2) and range (−∞,∞)
The correct Answer is:A→q;B→r
y=1+2x is linear function, therefore it is one-one and its range is (−π+1,π+1). Therefore (1 + 2x) is one-one but not onto so (A)→(q). Again, see the figure.
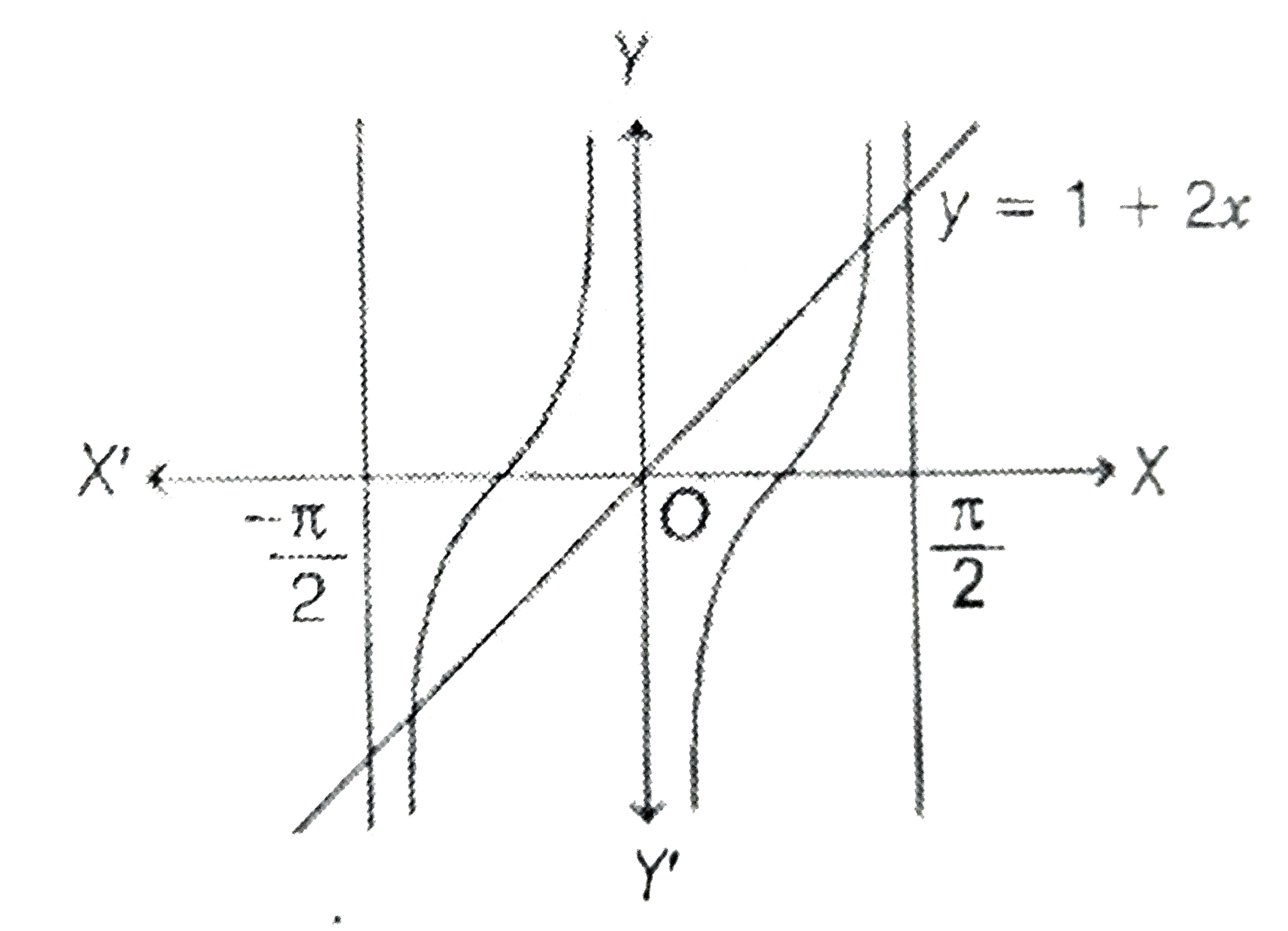
It is clear from the graph that y = tan x is one-one and onto, therefore (B)→(r).
Topper's Solved these Questions
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - FUNCTIONSEXERCISE - INVERSE AND PERIODIC FUNCTIONS11videos
FUNCTIONS
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - FUNCTIONSEXERCISE - COMPOSITE OF FUNCTIONS19videos
FUNCTIONS
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - ELLIPSEEXERCISE - EQUATION OF CHORD OF CONTACT, CHORD BISECTED AT A GIVEN POINT & DIAMETER3videos
ELLIPSE
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - HYPERBOLAEXERCISE - EQUATION OF CHORD OF CONTACT,CHORD BISECTED DIAMETER,ASYMPTOTE AND RECTENGULAR HYPERBOLA3videos
HYPERBOLA
Similar Questions
Match the conditions/ expressions in Column I with statements in Column II.
Let the functions defined in Column I have domain (−π/2,π/2).
(##41Y_SP_MATH_C10_E02_025_Q01.png" width="80%">View SolutionLet the function f'(x)=sinx be one- one and onto. Then a possible domain of f is
O [0,2π]
O [0,π]
O [−π2,π2]
O [−π,π]View Solution
Knowledge Check
- Question 1 - Select One
If function f(x) = (1+2x) has the domain (−π2,π2) and co-domain (−∞,∞) then function is
AOne-one ontoBOne-one but not ontoCMany-one but not ontoDMany-one onto - Question 2 - Select One
Let f be a function defined on [−π2,π2] by f(x) = 3cos4x−6cos3x−6cos2x−3. Then the range of f(x) is
A[−12,−3]B[−6,−3]C[−6,3]D(−12,3] - Question 3 - Select One or More
Let the domain and range of inverse circular functions are defined as follows:

If xε(−π2,π2),cosec−1cosecx isA2π−xBπ+xCπ−xD−π−x
f(x)=∫(2−11+x2−1√1+x2)dx then f is (A) increasing in (0,π) and decreasing in (−∞,0) (B) increasing in (−∞,0) and decreasing in (0,∞) (C) increasing in (−∞,∞) and (D) decreasing in (−∞,∞)
View SolutionLet f(x) be a increasing function defined on (0, ∞). If f(2a2+a+1)>f (3a2−4a+1). Find the range of a.
View SolutionThe number of real solutions of the equation sin−1(∞∑i=1xi+1−x∞∑i=1(x2)i)=π2−cos−1(∞∑i=1(−x2)i−∞∑i=1(−x)i) lying in the interval (−12,12) is ____. (Here, the inverse trigonometric function =sin−1x and cos−1x assume values in [π2,π2] and [0, π] , respectively.)
View SolutionThe range of f(x)=sin3x in domain [−π2,π2] is
View SolutionLet the function g:(−∞,∞)→(−π/2,π/2) be given by g(u) =2tan−1(eu)−π2 Then g is
View Solution

