Let $f (x) = \int e^{x} (x - 1) (x - 2) d x .$ Then $f$ decreases in the interval $(- \infty, - 2)$ (b) $- 2, - 1)$ $(1, 2)$ (d) $(2, + \infty)$

A

$(- \infty, - 2)$

B

$(- 2, - 1)$

C

$(1, 2)$

D

$(2, \infty)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Let $f (x) = \int e^{x} (x - 1) (x - 2) d x$
$\Rightarrow f' (x) = e^{x} (x - 1) (x - 2)$

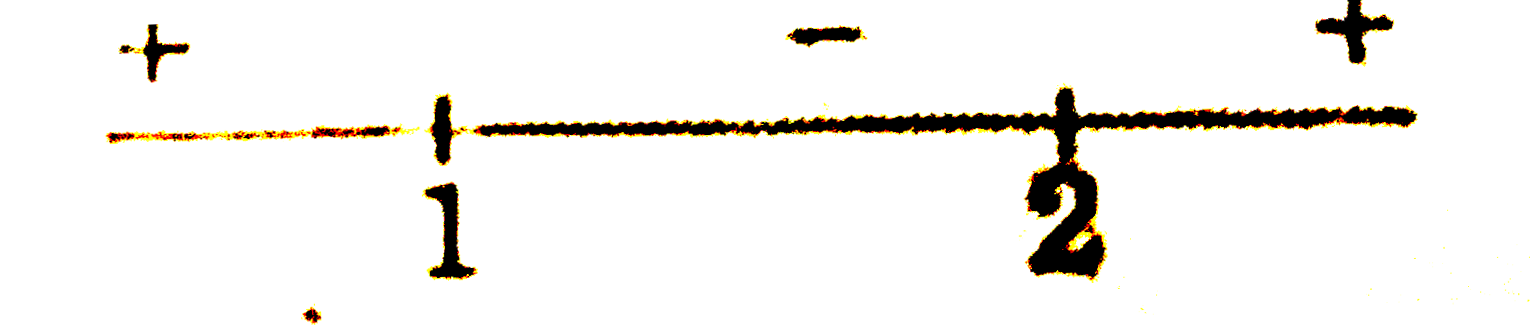
$∴ f' (x) < 0$ for $1 < x < 2$
$\Rightarrow f (x)$ is decreasing for $x \in (1, 2)$ .

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF DERIVATIVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Let f(x) = $\int e^{x} (x - 1) (x - 2) d x$ . Then f decreases in the interval
A $(- \infty, - 2)$
B $(- 2, - 1)$
C(1,2)
D $(2, \infty)$
Question 2 - Select One
Let $f (x) = \int e^{x} (x - 1) (x - 2) d x,$ then f(x) decrease in the interval
A $(- \infty, - 2)$
B(-2,-1)
C(1,2)
D $(2, \infty)$

IIT JEE PREVIOUS YEAR-APPLICATION OF DERIVATIVES -RATE MEASURE, INCREASING AND DECREASING FUNCTIONS (OBJECTIVE QUESTIONS I)

Home
Ask Doubt
Profile