The number of points in $(- \infty, \infty),$ for which $x^{2} - x sin x - cos x = 0,$ is

A

6

B

4

C

2

D

0

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Here , $x^{2} = x sin x + cos x$

Let $f (x) = x^{2} and g (x) = x sin x + cos x$
We know that, the graph for $f (x) = x^{2}$
To plot, $g (x) = x sin x + cos x$
$g' (x) = x cos x + sin x - sin x$
$g' (x) = cos x ... (i)$
$g'' (x) = - x sin x + cos x . . (i i)$
Put $g' (x) 0 \to x cos x = 0$
$∴ x = 0, \frac{π}{2}, \frac{3 π}{2}, \frac{5 π}{2}, \frac{7 π}{2}$

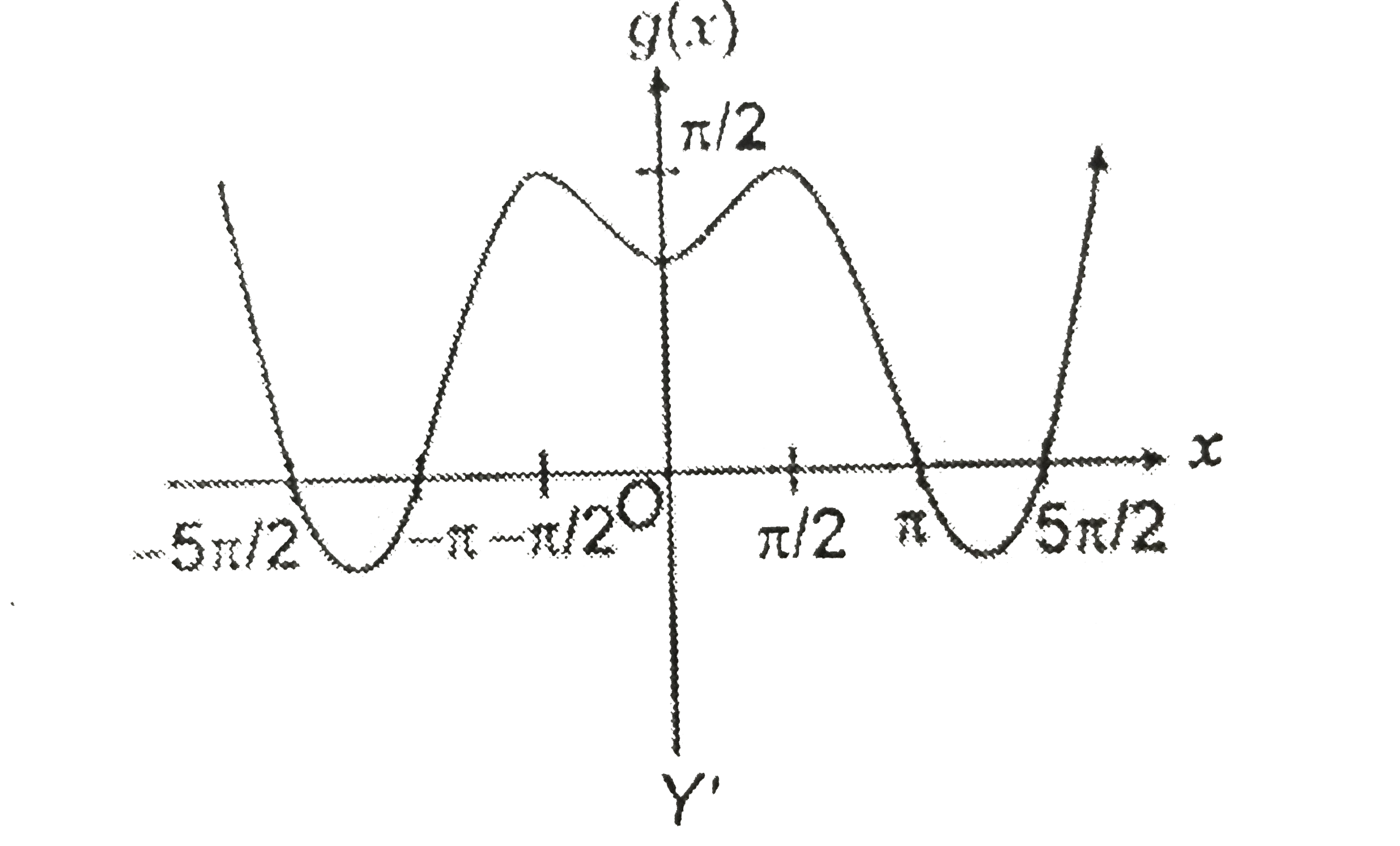
At $x = 0, \frac{3 π}{2}, \frac{7 π}{2}, ... ., f'' (x) > 0$ , so minimum
At $x = \frac{π}{2}, \frac{5 π}{2}, \frac{9 π}{2}, ..., f' (x) < 0$ , so maximum
So, graph of f(x) adn g(x) are shown as

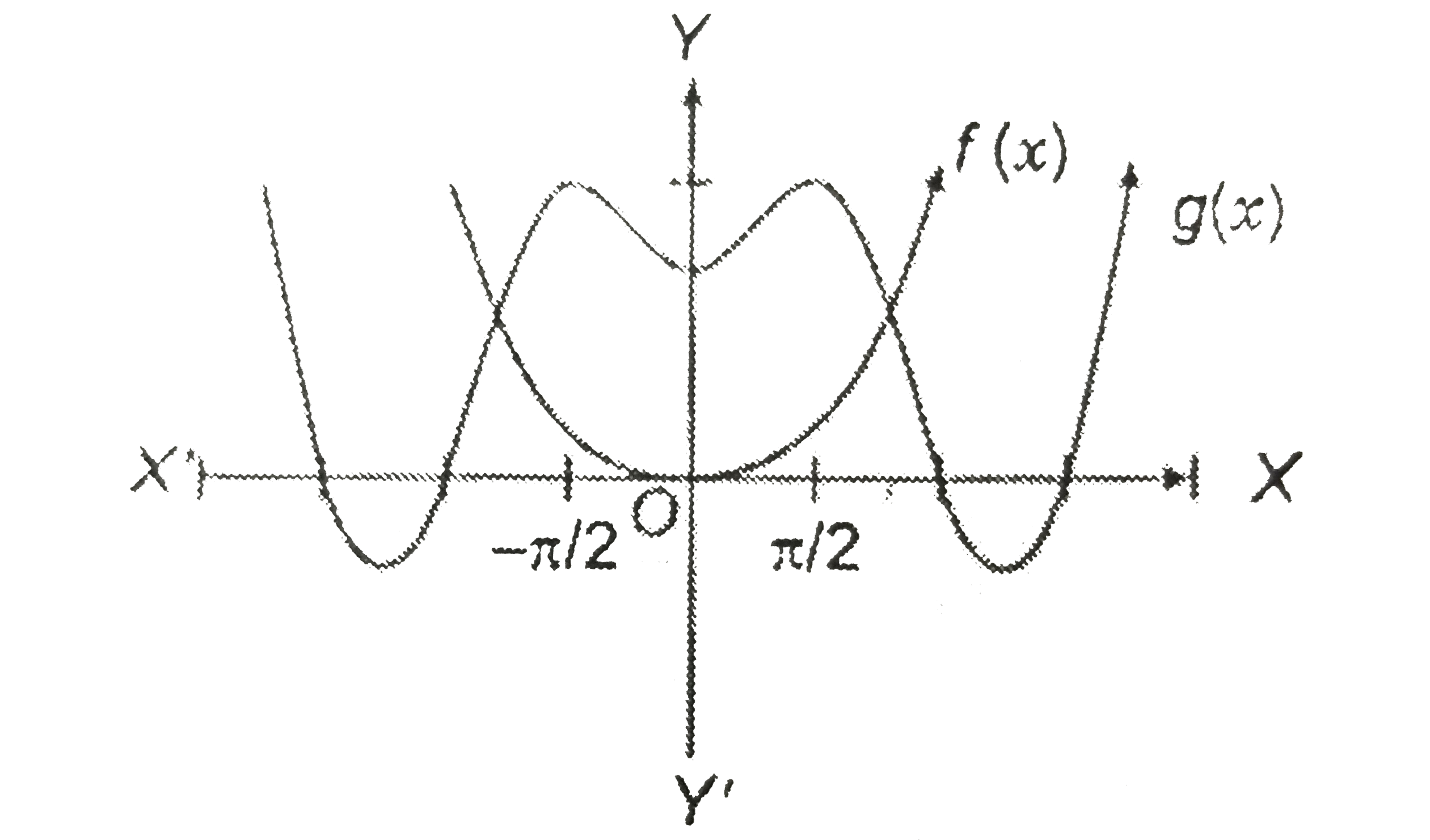
So, number of solution are 2.

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF DERIVATIVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The number of points in $(- \infty, \infty)$ for which $x^{2} - x sin x - cos x = 0,$ is
A6
B4
C2
D0
Question 2 - Select One
Let $f (x) < 0 \forall x \in (- \infty, 0) and f (x) > 0 \forall x \in (0, \infty)$ also $f (0) = 0,$ Again $f' (x) < 0 \forall x \in (- \infty, - 1) and f' (x) > \forall x \in (- 1, \infty)$ also $f' (- 1) = 0$ given $lim x \to \infty f (x) = 0 and lim x \to \infty f (x) = \infty$ and function is twice differentiable.
The minimum number of points where $f' (x)$ is zero is:
A1
B2
C3
D4
Question 3 - Select One
If $f : [0, \infty) \to [0, \infty)$ is a function with $f (0) = 0$ and $f' (x) > 1 \forall x \in (0, \infty)$ then number of solution(s) of the equation f (x) = f' (x) is
A0
B1
C2
Dinfinite

IIT JEE PREVIOUS YEAR-APPLICATION OF DERIVATIVES -MAXIMA AND MINIMA (OBJECTIVE QUESTIONS I)

Home
Ask Doubt
Profile