A rectangular sheet of fixed perimeter with sides having their lengths in the ratio $8 : 15$ is converted into anopen rectangular box by folding after removing squares of equal area from all four corners. If the total area of removed squares is 100, the resulting box has maximum volume. Then the length of the sides of the rectangular sheet are 24 (b) 32 (c) 45 (d) 60

A

$24$

B

$32$

C

$45$

D

$60$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, C

The problem is based on the concept to maximise volume of cuboid i.e. to form a function of volume, say $f (x)$ find $f' (x) and f'' (x)$ .
Put $f' (x) = 0 and$ check $f'' (x)$ to be + ve or - ve for minimum and maximum, respectively.
Here, $l = 15 x - 2 a, b = 8 x - 2 a and h = a$

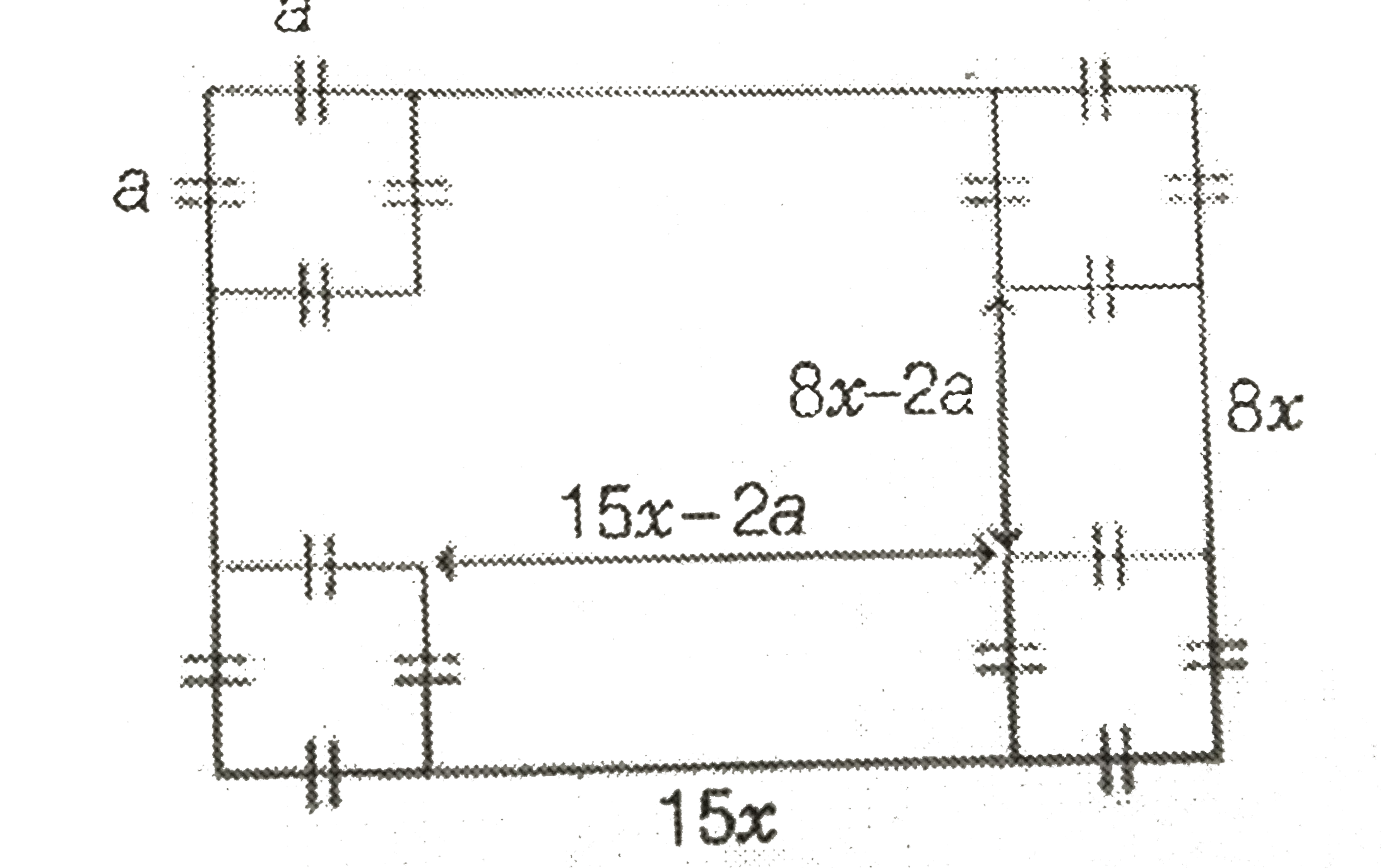
$∴$ Volume = $(8 x - 2 a) (15 x - 2 a) a$
$V = 2 a \cdot (4 x - a) (15 x - 2 a)$ ... (i)

On differentiating Eq. (i) w.r.t a, we get
$\frac{d v}{d a} = 6 a^{2} - 46 a x = 60 x^{2}$
Again, differentiating,
$\frac{d^{2} v}{d a^{2}} = 12 a - 46 x$
Here, $(\frac{d v}{d a}) = 0 \Rightarrow 6 x^{3} - 23 x + 15 = 0$
At $a = 5 \Rightarrow x = 3, \frac{5}{6}$
$\Rightarrow (\frac{d^{2} v}{d a^{2}}) = 2 (30 - 23 x)$
At $x = 3 (\frac{d^{2} v}{d a^{2}}) = 2 (30 - 69) < 0$
$∴$ Maximum when $x = 3$ , also at $x = \frac{5}{6} \Rightarrow (\frac{d^{2} v}{d a^{2}}) > 0$
$∴$ At $x = 5 / 6$ , volume is minimum.
Thus, sides are $8 x = 24 and 15 x = 45$

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF DERIVATIVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
A rectangular sheet of fixed perimeter with sides having their lengths in the ratio 8 : 15 is converted into an open rectangular box by folding after removing squares of equal area from all four corners. If the total area of removed squares is 100, the resulting box has maximum volume. The lengths of the sides of the rectangular sheet are :
A24
B32
C45
D60
Question 2 - Select One
A rectangular sheet of fixed perimeter with sides having their lengths in the ratio 8:15 is converted into an open rectangular box by folding after removing squares of equal area from all four corners if the total area of removed squares is 100 the resulting box has maximum volume the lengths of the sides of the rectangular sheet are
A24
B32
C45
D60
Question 3 - Select One or More
A rectangular sheet of fixed perimeter with sides having their lengths in the ratio 8 : 15 is converted into an open rectangular box by folding after removing squares of equal area from all four corners. If the total area of removed squares is 100, the resulting box has maximum volume. The lengths of the sides of the rectangular sheet are :
A $24$
B $32$
C $45$
D $50$

IIT JEE PREVIOUS YEAR-APPLICATION OF DERIVATIVES -MAXIMA AND MINIMA (OBJECTIVE QUESTIONS II)

Home
Ask Doubt
Profile