According to Bohr's theory, Ea=Total energy , Ka=Kinetic energy , Vn=Potential energy , rn=Radius of nth orbit
Match the following
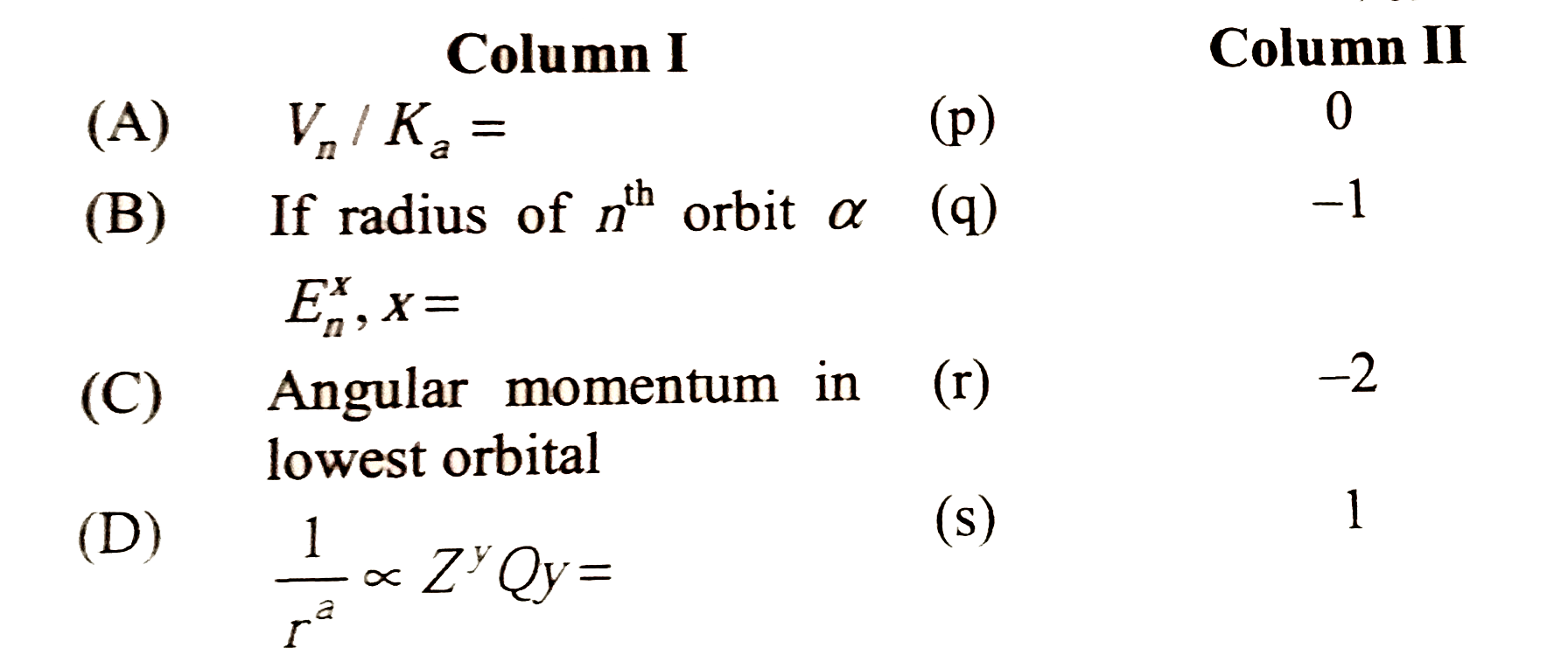
According to Bohr's theory, Ea=Total energy , Ka=Kinetic energy , Vn=Potential energy , rn=Radius of n^

Text Solution
Verified by Experts

The correct Answer is:A→r;B→q;C→p;D→s

According to Bohr's theory
Total energy is En=Kn+Vn
Kinetic energy =Kn=18πε0.Ze2r
Potential energy =Vn=14πε0.Ze2r
∴En=18πε0.Ze2r−14πε0.Ze2r
Radius of nth orbit (rn)=n2h2ε0πmZe2∴En=−me48ε20h2×1n2
(A)VnKn=−14πε0.Ze2r18πε0.Ze2r=−2
(B)En∝1n2or En∝1rn
Radius of nth orbit rn∝Exn ∴x=−1
(C)Angular momentum =h2π√l+(l+1),l=0,1,2..
For the lower orbit n=1
∴ l=0 and m=0
Hence angular momentum of lowest orbit
=h2π√0(0+1)=0
(D)1rn∝Zyasrn∝1Z ∴y=1

Updated on:21/07/2023
Doubtnut Promotions Banner
|
Class 11CHEMISTRYSTRUCTURE OF ATOM

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • A satellite has kinetic energy K, potential energy V and total energy E. Which of the following statements is true?

    AK=-V/2
    BK=V/2
    CE=K/2
    DE=-K/2

  • According to Bohr's theory, the electronic energy of H-atom in Bohr's orbit is given by

    AEn=−2.18×10−19×Z2n2J
    BEn=−2.179×10−18×Z2n2J
    CEn=−21.79×10−18×Z2n2J
    DEn=−21.8×10−21×Z2n2J

  • According to Bohr's theory, the electronic energy of H-atom in Bohr's orbit is given by

    AEn=−2.18×10−19×Z2n2J
    BEn=−2.179×10−18×Z2n2J
    CEn=−21.79×10−18×Z2n2J
    DEn=−21.8×10−21×Z2n2J