(a) Look at the following matchstick pattern of squares (Fig 11.6). The squares are not separate. Two neighbouring squares have a common matchstick. Observe the patterns and find the rule that gives the number of matchsticks in terms of the number of squares. (Hint : If you remove the vertical stick at the end, you will get a pattern of Cs.)(b) Fig 11.7 gives a matchstick pattern of triangles. As in Exercise 11 (a) above, find the general rule that gives the number of matchsticks in terms of the number of triangles.

a) By observing the pattern
carefully,itcanbeconcludedthatthenumberofmatchsticks is 4,7,10,and
13which is 1 morethanthricethe numberofsquarespresent
i.e, 1 square =3×1+1=4matchsticks, 2 squares =3×2+1=7
matchsticks and so on..
Thus, the rule for this pattern
= 3n + 1 where,n=numberofsquares
b) Similarly, by observing the above matchstick pattern of
triangles, we can conclude that every consecutive triangle shares a
common matchstick.
Thenumberofmatchsticks in the first pattern is 3, i.e,2×1+1=3
The number of matchsticks in the second pattern is 5, i.e,2×2+1=5
The number of matchsticks in the third pattern is 7, i.e,2×3+1=7
Thus, the pattern generated is adding 1 matchstick to
twice the number of triangles present
Hence, the general rule for the pattern of triangles is 2n+1
where, n = number of triangles
Topper's Solved these Questions
Similar Questions
Look at the following matchstick pattern of squares (see fig.). The squares are not separate. Two neighbouring squares have a common matchstick. Observe the patterns and find the rule that gives the number of matchsticks in terms of the number of squares. (Hint: If you remove the vertical stick at the end, you will get a pattern of Cs.)

 View Solution
View SolutionThe given figure gives a matchstick pattern of triangles. As in above, find the general rule that gives the number of matchsticks in terms of the number of triangles.
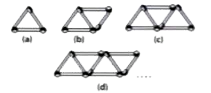 View Solution
View SolutionFind the number of matchsticks used in nth pattern.
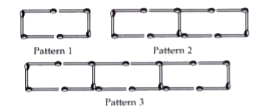 View Solution
View SolutionFind out the number of squares in the given pattern.
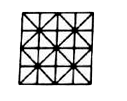 View Solution
View SolutionFind out the number of squares in the given pattern.
 View Solution
View SolutionFind out the number of squares in the given pattern.
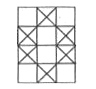 View Solution
View SolutionFind the pattern followed in given figure and the number of matchsticks used in 86th figure.
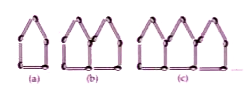 View Solution
View SolutionHow does a matchstick catch fire?
View SolutionDescribe the history of a matchstick.
View SolutionFind the number of dots in the pattern 143 of the following pattern.
 View Solution
View Solution

