Let S= set of point inside the sqare, T= set of points inside the triangles and C= the set of point inside the circle, if the triangle and circle intersect each other are contained in the square, then S∩T∩C=φ b. S∩T∩C=C c. S∪T∪C=S d. S∪T∩C=C
Step by step video & image solution for Let S= set of point inside the sqare, T= set of points inside the triangles and C= the set of point inside the circle, if the triangle and circle intersect each other are contained in the square, then SnnTnnC=varphi b. SnnTnnC=C c. SuuTuuC=S d. SuuTnnC=C by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Let S= set of point inside the sqare, T= set of points inside the triangles and C= the set of point inside the circle, if the triangle and circle intersect each other are contained in the square, then S∩T∩C=φ b. S∩T∩C=C c. S∪T∪C=S d. S∪T∩C=C
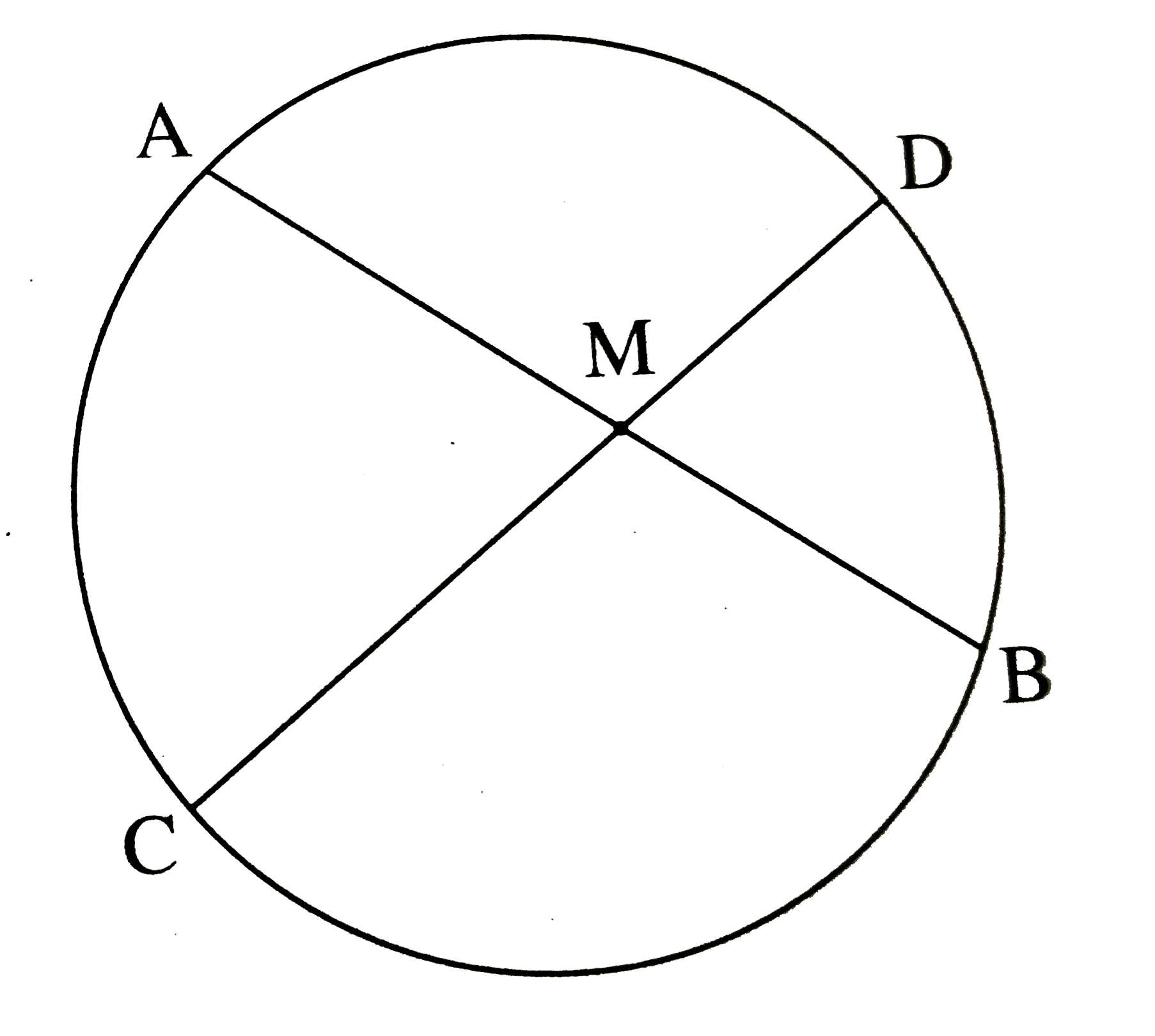
View SolutionChords AB and CD intersect at point M inside the circle then theorem of internal division of chords.
AM×BM=□×□
View Solution
Knowledge Check
Let O be a point inside ΔABC such that
∠OAB=∠OBC=∠OCA=θ
cotA+cotB+cotC is equal toAtan2θBcot2θCtanθDcotθ
Let R be set of points inside a rectangle of sides a and b (a,b>1) with two sides along the positive direction of x-axis and y-axis
View SolutionThe circle x2+y62−6x−10y+c=0 does not touch and intersect the coordinate axes and the point (1,4) is inside the circle. find the set of values of c.
View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and the other circle at B and D. Prove the AC|| BD
View SolutionIf area of the triangle with the points A,B and C is equal to zero then the points A,B,C are
View SolutionIf area of the triangle with the points A,B and C is equal to zero then the points A,B,C are
View SolutionLet C be the curve y3−3xy+2=0. If H is the set of points on the curve C, where the tangent is horizontal and V is the set of points on the curve C, where the tangent is vertical, then H = … and V = … .
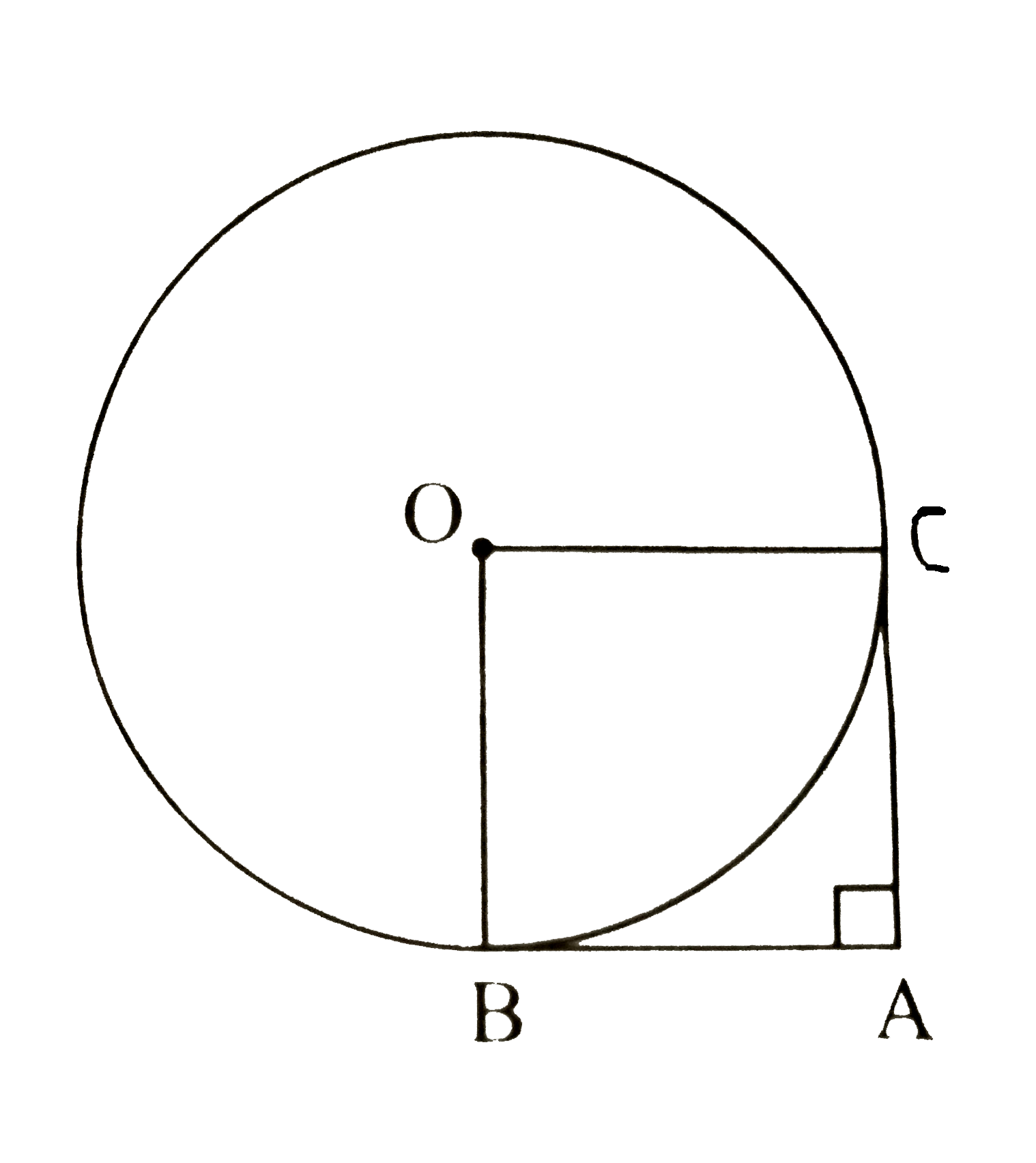
View SolutionIn the figure,tangents at B and C of the circle with centre O intersect at point A. If ∠BAC=90∘ then prove □BACO is a square
View Solution
