నీ తరగతి విద్యార్థులతో మంగళవారం పాఠశాలకు హాజరుకాని వారిని సమితి A అని,బుధవారం హాజరుకాని విద్యార్థుల సమితి B అనుకొందాం. అపుడు A={రోజా, రాము,రవి} మరియు B={రాము,ప్రీతి,హనీఫ్} ఇపుడు మనం మంగళవారం లేక బుధవారం పాఠశాలకు హాజరుకాని విద్యార్థుల సమితి K, అనుకుంటే అపుడు రోజా ∈K అవుతుందా? రాము ∈K అవుతుందా? రవి ∈K అవుతుందా? హనీఫ్ ∈K అవుతుందా? ప్రీతి ∈K అవుతుందా? అఖిల ∈K అవుతుందా?
Step by step video & image solution for నీ తరగతి విద్యార్థులతో మంగళవారం పాఠశాలకు హాజరుకాని వారిని సమితి A అని,బుధవారం హాజరుకాని విద్యార్థుల సమితి B అనుకొందాం. అపుడు A={రోజా, రాము,రవి} మరియు B={రాము,ప్రీతి,హనీఫ్} ఇపుడు మనం మంగళవారం లేక బుధవారం పాఠశాలకు హాజరుకాని విద్యార్థుల సమితి K, అనుకుంటే అపుడు రోజా in K అవుతుందా? రాము in K అవుతుందా? రవి in K అవుతుందా? హనీఫ్ in K అవుతుందా? ప్రీతి in K అవుతుందా? అఖిల in K అవుతుందా? by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
క్రింది వాటిలో ఏవి సమితులు? మీ సమాధానాన్ని సహేతుకంగా సమర్థించండి. "J" అనే అక్షరంతో ప్రారంభమయ్యే ఒక సంవత్సరంలో గల అన్నీ నెలల సమూహాలు.
View Solutionఘటన E యొక్క సంభావ్యత + ఘటన E కాదు సంభావ్యత =..............
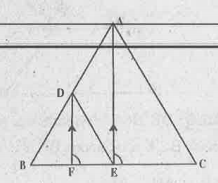
View Solutionఇచ్చిన పటంలో, DE∣∣AC మరియు DF∣∣AE అయిన BF /FE = BE/ EC అని చూపండి.
View SolutionIf limn→∞1(2n−1)k+2(2n−2)k+3(2n−3)k+...+n.nknk+1=2k+a−2k+1+1−2k+bk+2where a,b,k∈N and k≥5 then the value of a+b3 is
View SolutionIf limn→∞1(2n−1)k+2(2n−2)k+3(2n−3)k+...+n.nknk+1=2k+a−2k+1+1−2k+bk+2where a,b,k∈N and k≥5 then the value of a+b3 is
View SolutionIf limn→∞1(2n−1)k+2(2n−2)k+3(2n−3)k+...+n.nknk+1=2k+a−2k+1+1−2k+bk+2where a,b,k∈N and k≥5 then the value of a+b3 is
View SolutionIf limn→∞1(2n−1)k+2(2n−2)k+3(2n−3)k+...+n.nknk+1=2k+a−2k+1+1−2k+bk+2where a,b,k∈N and k≥5 then the value of a+b3 is
View SolutionIf limn→∞1(2n−1)k+2(2n−2)k+3(2n−3)k+...+n.nknk+2=2k+a−2k+1+1−2k+bk+2where a,b,k∈N and k≥5 then the value of a+b3 is
View SolutionIf limn→∞1(2n−1)k+2(2n−2)k+3(2n−3)k+...+n.nknk+1=2k+a−2k+1+1−2k+bk+2where a,b,k∈N and k≥5 then the value of a+b3 is
View SolutionIf limn→∞1(2n−1)k+2(2n−2)k+3(2n−3)k+...+n.nknk+1=2k+a−2k+1+1−2k+bk+2where a,b,k∈N and k≥5 then the value of a+b3 is
View SolutionIf limn→∞1(2n−1)k+2(2n−2)k+3(2n−3)k+...+n.nknk+1=2k+a−2k+1+1−2k+bk+2where a,b,k∈N and k≥5 then the value of a+b3 is
View SolutionIf limn→∞1(2n−1)k+2(2n−2)k+3(2n−3)k+...+n.nknk+1=2k+a−2k+1+1−2k+bk+2where a,b,k∈N and k≥5 then the value of a+b3 is
View SolutionIf limn→∞1(2n−1)k+2(2n−2)k+3(2n−3)k+...+n.nknk+1=2k+a−2k+1+1−2k+bk+2where a,b,k∈N and k≥5 then the value of a+b3 is
View SolutionIf limn→∞1(2n−1)k+2(2n−2)k+3(2n−3)k+...+n.nknk+1=2k+a−2k+1+1−2k+bk+2where a,b,k∈N and k≥5 then the value of a+b3 is
View SolutionIf limn→∞1(2n−1)k+2(2n−2)k+3(2n−3)k+...+n.nknk+1=2k+a−2k+1+1−2k+bk+2where a,b,k∈N and k≥5 then the value of a+b3 is
View SolutionIf limn→∞1(2n−1)k+2(2n−2)k+3(2n−3)k+...+n.nknk+1=2k+a−2k+1+1−2k+bk+2where a,b,k∈N and k≥5 then the value of a+b3 is
View Solution
