క్రింది వాక్యాలకు తగు కారణాలు పేర్కొనండి. {2,4,6,8,10}≠{x:x =2n+1 మరియు x∈N}
Step by step video & image solution for క్రింది వాక్యాలకు తగు కారణాలు పేర్కొనండి. {2,4,6,8,10}!={x:x =2n+1 మరియు x in N} by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
క్రింది వాటిలో ఏవి సమితులు? మీ సమాధానాన్ని సహేతుకంగా సమర్థించండి. "J" అనే అక్షరంతో ప్రారంభమయ్యే ఒక సంవత్సరంలో గల అన్నీ నెలల సమూహాలు.
View Solutionఘటన E యొక్క సంభావ్యత + ఘటన E కాదు సంభావ్యత =..............
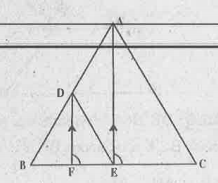
View Solutionఇచ్చిన పటంలో, DE∣∣AC మరియు DF∣∣AE అయిన BF /FE = BE/ EC అని చూపండి.
View SolutionD = {x:x=2n-1 < 20 and n ∈N }
View SolutionIf A={x:x=2n+1, n∈Z} and B={x:x=2n, n∈Z} , then A∪B={x:x is an odd integer} ∪{x:x is an even integer}={x:x is an integer}=Z.
View SolutionLet A={x:x∈N}, B={x;x2n, n∈N}, C={x:x=2n−1,n∈N}and, D={x:x is a prime natural number} . Find: A∩B
View SolutionLet A={x:x∈N}, B={x;x2n, n∈N}, C={x:x=2n−1,n∈N}and, D={x:x is a prime natural number} . Find: A∩C
View SolutionLet A={x:x∈N}, B={x;x2n, n∈N}, C={x:x=2n−1,n∈N}and, D={x:x is a prime natural number} . Find: A∩D
View SolutionLet A={x:x∈N}, B={x;x=2n, n∈N}, C={x:x=2n−1,n∈N}and, D={x:x is a prime natural number} . Find: B∩C
View SolutionLet A={x:x∈N}, B={x;x2n, n∈N}, C={x:x=2n−1,n∈N}and, D={x:x is a prime natural number} . Find: B∩D
View SolutionLet A={x:x∈N}, B={x;x=2n, n∈N}, C={x:x=2n−1,n∈N}and, D={x:x is a prime natural number} . Find: C∩D
View SolutionList all the elements of each of the sets given below:
(i) A={x:x=2n,n∈Nandn≤5}.
(ii) B={x:x=2n+1,n∈Wandn<5}.
(iii) C={x:x=nn,n∈Nandn<6}.
(iv) D={x:x=n2,n∈Nand2≤n≤5}.
(v) E={x:x∈Zandx2=x}.
(vi) F={x:x∈Zand12<x132}.
(vii) G={x:x=1(2n−1),n∈Nand1≤n≤5}.
(viii) H={x:x∈Z,|x|≤2}.
View SolutionLet A={x:x∈N},B={x:x∈2n,n∈N},C={x:x=2n−1,n∈N}and D= {x:x is a prime number} then____
A∩C is
View SolutionLet A={x:x∈N},B={x:x∈2n,n∈N},C={x:x=2n−1,n∈N}and D= {x:x is a prime number} then____
B∩C is
View SolutionIf A={x:x=3n−2n−1,n∈N}andB={x:x=4(n−1),n∈N}. Then
View Solution
