A={x : x, 6 కన్నా తక్కువైన సహజ సంఖ్య }, B={x : x,60 ను భాగించు ఒక ప్రధాన సంఖ్య }, C={x : x,10 కంటే తక్కువైన ఒక బేసి సహజ సంఖ్య }, D={x : x, 48 ను భాగించు ఒక సరి సహజ సంఖ్య}, అయిన వీటికి రోస్టర్ రూపం రాసి D - B లను కనుక్కోండి.
Step by step video & image solution for A={x : x, 6 కన్నా తక్కువైన సహజ సంఖ్య }, B={x : x,60 ను భాగించు ఒక ప్రధాన సంఖ్య }, C={x : x,10 కంటే తక్కువైన ఒక బేసి సహజ సంఖ్య }, D={x : x, 48 ను భాగించు ఒక సరి సహజ సంఖ్య}, అయిన వీటికి రోస్టర్ రూపం రాసి D - B లను కనుక్కోండి. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
క్రింది వాటిలో ఏవి సమితులు? మీ సమాధానాన్ని సహేతుకంగా సమర్థించండి. "J" అనే అక్షరంతో ప్రారంభమయ్యే ఒక సంవత్సరంలో గల అన్నీ నెలల సమూహాలు.
View Solutionఘటన E యొక్క సంభావ్యత + ఘటన E కాదు సంభావ్యత =..............
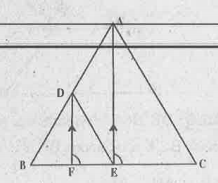
View Solutionఇచ్చిన పటంలో, DE∣∣AC మరియు DF∣∣AE అయిన BF /FE = BE/ EC అని చూపండి.
View Solution(x−a)(x−b)(x−c)(x−d)=Ax−c−Bx−d+C⇒C=
View SolutionMnO−24+Cl_2−−→MnO_4^-+Cl^- సమీకరణాన్ని ఆక్సీకరణ సంఖ్య పద్ధతిలో తుల్యం చేయండి.
View Solutionf(x) ను (x−a) చే భాగించగ వచ్చు శేషం
View Solutionx3+1 ను (x+1) చే భాగించగ వచ్చు శేషమును భాగహార పద్దతిలో కనుగొనండి.
View SolutionA={x : x ∈ N మరియు x < 20}, B={x : x ∈ N మరియు x le 5} అయిన సమితి A - B కి నిర్మాణ రూపం రాయండి.
View SolutionA={x : x, 6 కన్నా తక్కువైన సహజ సంఖ్య }, B={x : x,60 ను భాగించు ఒక ప్రధాన సంఖ్య }, C={x : x,10 కంటే తక్కువైన ఒక బేసి సహజ సంఖ్య }, D={x : x, 48 ను భాగించు ఒక సరి సహజ సంఖ్య}, అయిన వీటికి రోస్టర్ రూపం రాసి A∪B
View SolutionA={x : x, 6 కన్నా తక్కువైన సహజ సంఖ్య }, B={x : x,60 ను భాగించు ఒక ప్రధాన సంఖ్య }, C={x : x,10 కంటే తక్కువైన ఒక బేసి సహజ సంఖ్య }, D={x : x, 48 ను భాగించు ఒక సరి సహజ సంఖ్య}, అయిన వీటికి రోస్టర్ రూపం రాసి B∩C
View SolutionA={x : x, 6 కన్నా తక్కువైన సహజ సంఖ్య }, B={x : x,60 ను భాగించు ఒక ప్రధాన సంఖ్య }, C={x : x,10 కంటే తక్కువైన ఒక బేసి సహజ సంఖ్య }, D={x : x, 48 ను భాగించు ఒక సరి సహజ సంఖ్య}, అయిన వీటికి రోస్టర్ రూపం రాసి A - D
View SolutionA={1,2,3,4} అయిన A యొక్క ఉపసమితుల సంఖ్య
View SolutionA={2,3,4,5,6} అయిన A కి గల ఉపసమితుల సంఖ్య
View SolutionA={2,6} అయిన A కి గల ఉపసమితుల సంఖ్య
View SolutionA={x,y,z} అయిన A కి గా ఉపసమితుల సంఖ్య
View Solution
