సమద్విబహు త్రిభుజము ABC లో లంబకోణము C వద్ద కలదు. అయిన అని చూపండి.
Step by step video & image solution for సమద్విబహు త్రిభుజము ABC లో లంబకోణము C వద్ద కలదు. అయిన AB^(2) = 2AC^(2) అని చూపండి. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- సరూప త్రిభుజాలుBOOK - VGS PUBLICATION-BRILLIANT(TELUGU)CHAPTER - సరూప త్రిభుజాలుEXERCISE - Exercise
211 Videos
- సమితులుBOOK - VGS PUBLICATION-BRILLIANT(TELUGU)CHAPTER - సమితులుEXERCISE - Exercise
298 Videos
- సాంఖ్యకశాస్తంBOOK - VGS PUBLICATION-BRILLIANT(TELUGU)CHAPTER - సాంఖ్యకశాస్తంEXERCISE - Exercise
147 Videos
Similar Questions
ఇచ్చిన పటంలో, DE∣∣AC మరియు DF∣∣AE అయిన BF /FE = BE/ EC అని చూపండి.
View Solutionక్రింది వాటిలో ఏవి సమితులు? మీ సమాధానాన్ని సహేతుకంగా సమర్థించండి. "J" అనే అక్షరంతో ప్రారంభమయ్యే ఒక సంవత్సరంలో గల అన్నీ నెలల సమూహాలు.
View Solutionఒక' గ్రామంలో కొంతమంది విద్యార్థుల జట్టు “పర్యావరణ పరిరక్షణ - అవగాహని అనే కార్యక్రమంలో భాగంగా, 20 ఇండ్లలో సర్వే నిర్వహించి, ఎన్నెన్ని మొక్కలు నాటినారో సమాచారాన్ని సేకరించి, ఈ క్రింది పట్టికలో నమోదు చేసినారు. సగటున ఒక ఇంటికి ఎన్ని మొక్కలు నాటినారో కనుక్కోండి.

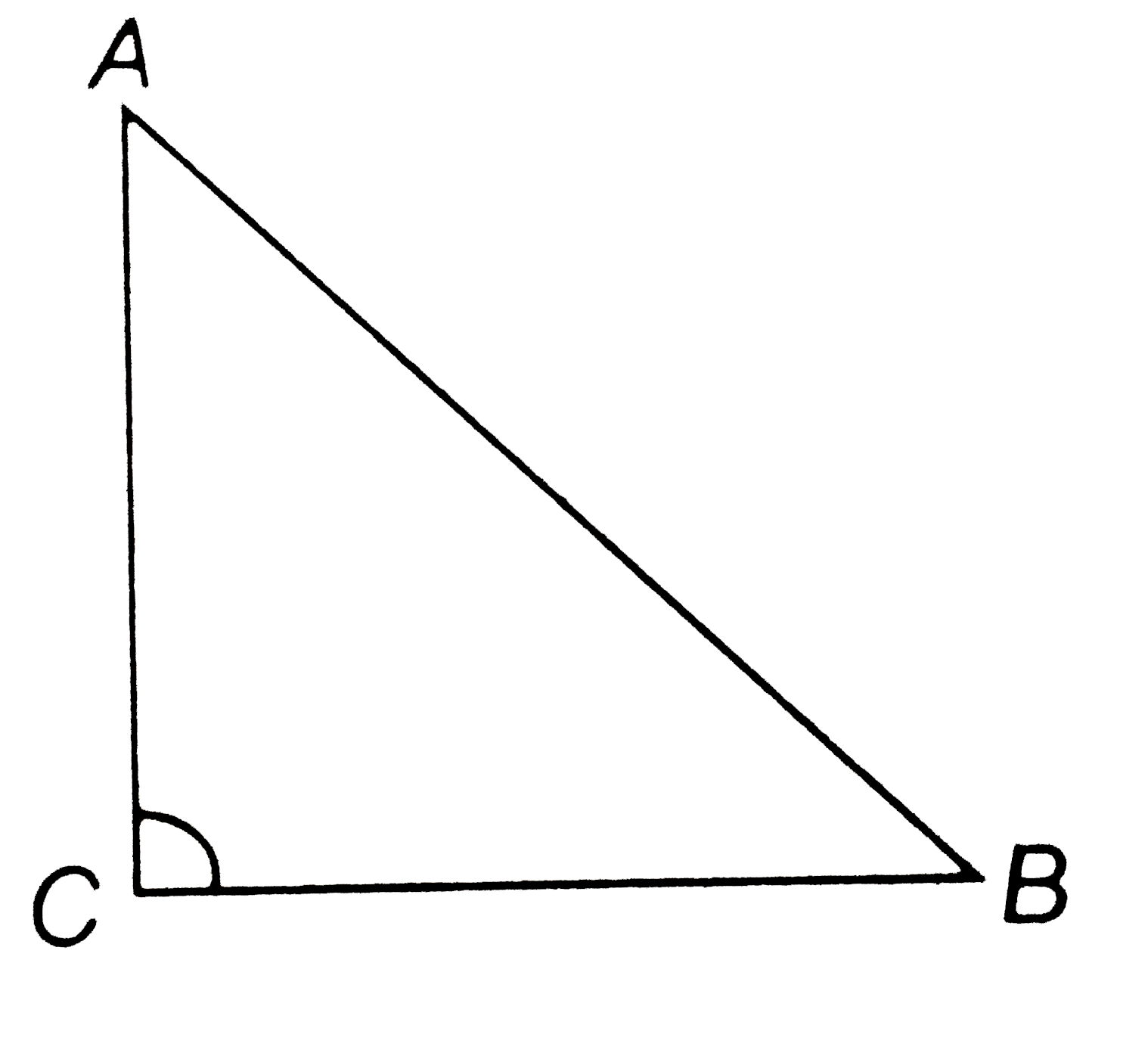
View SolutionABC is an isosceles right triangle right-angled at C . Prove that AB2=2AC2 .
View SolutionABC is an isosceles right triangle, right-angled at C . Prove that: AB2=2AC2.
View SolutionABC is a isosceles right angled triangle, right angled at C. prove that AB2=2AC2
View SolutionABC एक समद्विबाहु त्रिभुज है जिसका कोण c समकोण है । सिद्ध कीजिए कि AB2=2AC2 है ।
View SolutionIn an isosceles ΔABC, if AC=BC and AB2=2AC2 then ∠C=?
View SolutionABC एक समद्विबाहु समकोण त्रिभुज है जिसका कोण C समकोण है । सिद्ध कीजिए कि AB2=2AC2.
View Solution△ABC के समद्विबाहु त्रिभुज है जिसका ∠C समकोण है | सिद्ध कीजिए कि AB2=2AC2
View Solutionएक समद्विबाहु त्रिभुज ABC में, यदि AC=BC तथा AB2=2AC2 हो, तो ∠C=
View SolutionABC एक समद्विबाहु त्रिभुज है जिसका कोण C समकोण है सिद्ध कीजिये कि AB2=2AC2 है
View SolutionIn a triangle ABC, 2ac sin(A−B+C2) =
View SolutionABC ಯು ಸಮದ್ವಿಬಾಹು ತ್ರಿಭುಜದಲ್ಲಿ C ಯು ಲಂಬಕೋನವಾಗಿದೆ AB2=2AC2 ಎಂದು ಸಾಧಿಸಿ
View SolutionA={x : x ∈ N x < 6} మరియు B={x : x ∈ N మరియు 3<x<8}అయినA−B!= B - A అని వెన్ చిత్రాల ద్వారా చూపండి.
View Solution
