A అల్ప కోణం మరియు tanA=1√3 అయిన sin A=
12
1
√2
√32
Step by step video & image solution for A అల్ప కోణం మరియు tan A=1 /sqrt3 అయిన sin A= by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- త్రికోణమితిBOOK - VGS PUBLICATION-BRILLIANT(TELUGU)CHAPTER - త్రికోణమితిEXERCISE - Exercise
299 Videos
- క్షేత్రమితిBOOK - VGS PUBLICATION-BRILLIANT(TELUGU)CHAPTER - క్షేత్రమితిEXERCISE - Exercise
121 Videos
- త్రికోణమితి అనువర్తనాలుBOOK - VGS PUBLICATION-BRILLIANT(TELUGU)CHAPTER - త్రికోణమితి అనువర్తనాలుEXERCISE - Exercise
97 Videos
Similar Questions
ఒక లంబకోణ త్రిభుజం ABC లో భుజాలు AB, BC మరియు CA ల పొడవులు వరుసగా 8 సెంమీ, 15 సెంమీ, మరియు 17 సెంమీ అయిన sinA,cosA మరియు tan A ల విలువలు కనుగొనుము.
View Solutionక్రీడా వస్తువులను తయారుచేసే కంపెనీ షటిల్ కాక్ లను నిల్వ చేసేందుకు 100 స్థూపాకర కాగితపు డబ్బాలను తయారు చేయాలనుకోండి. స్థూపాకరపు డబ్బా యొక్క కొలతలు 35 సెంమీ. పొడవు/ఎత్తు మరియు భూవ్యాసార్థము 7 సెంమీ ఉండే విధముగా మూతలులేని 100 డబ్బాలను తయారు చేయడానికి కావలసిన కాగితపు పరిమాణము ఎంత?
View Solutionభూమన జక టవర్ నిటారుగా నిలిచి ఉంది. అ టవర అడుగు ముంది 15 మీటర్ల దూరదు మంది ఆ టవర్ పె కొన 45∘ ఊర్ధ్వకోణంలో పరిశీలించబడింది. ఆ టవర్ ఎత్తు ఎంత ?
View Solutionमूल्यांकन कीजिए
sin[tan−1(−√3)+cos−1(−√32)].
View SolutionIf a=sin−1(−√22)+cos−1(−12)andb=tan−1(−√3)−cot−1(−1√3), then
View SolutionThe value of sin ^(-1) (-(1)/(sqrt2)) + cos ^(-1) (-(1)/(2)) - tan ^(-1) (-sqrt3) + cot ^(-1) (-(1)/(sqrt3)) is
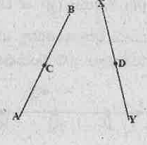
View SolutionIn the side map AC=XD, c మరియు D లు AB మరియు XY ల మధ్య బిందువులు. అయిన Show AB = XY.
View Solutionకింది పటంలో AC=XD, c మరియు D లు AB మరియు XY ల మధ్యబిందువులు వరుసగా అయిన AB మరియు XY లు .
View Solutionp(x)=x^(2)-5x+6, q(x)=x-2 మరియు r(x)=0 అయిన g(x)=
View SolutionS = {x,x అనేది 2n + 3, nవ పదంగా గల అంకథ్రేఢిలోని పదము, మరియు n<6) అయిన S=
View Solutiontan−1(1√3)−sin−1(12) is equal to :
View SolutionThe value of sin[tan−1(−√3)+cos−1(−√32)] is = ______
View SolutionFind the value of
tan−1(−1√3)+cot−1(1√3)+tan−1[sin(−π2)]
View SolutionShow that tan75∘=(√3)+1√3−1=2+√3. Hence deduce that tan75∘−cot75∘=4sin60∘.
View SolutionEvaluate : tan−1(−1√3)+cot−1(1√3)+tan−1(sin(−π2)).
View Solution
