Two containers contain two liquids A and B. The mass of liquid A is half the mass of liquid B. Both of them are heated to that extent so that the increase in the temperatures of the liquids is the same. The heat supplied for this purpose in liquid A is double that in the case of liquid B. Find out the ratio of the specific heat of A and B.

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem, we need to use the formula for heat supplied to a substance, which is given by:
$Q = m \cdot c \cdot Δ T$
where:
- $Q$ is the heat supplied,
- $m$ is the mass of the liquid,
- $c$ is the specific heat capacity of the liquid, and
- $Δ T$ is the change in temperature.
Let's denote:
- Mass of liquid A = $m_{A}$
- Mass of liquid B = $m_{B}$
- Specific heat of liquid A = $c_{A}$
- Specific heat of liquid B = $c_{B}$
- Change in temperature for both liquids = $Δ T$
Step 1: Define the masses
According to the problem, the mass of liquid A is half the mass of liquid B:
$m_{A} = \frac{1}{2} m_{B}$
Step 2: Write the heat equations
The heat supplied to liquid A is given by:
$Q_{A} = m_{A} \cdot c_{A} \cdot Δ T$
The heat supplied to liquid B is given by:
$Q_{B} = m_{B} \cdot c_{B} \cdot Δ T$
Step 3: Relate the heat supplied
It is given that the heat supplied to liquid A is double that supplied to liquid B:
$Q_{A} = 2 \cdot Q_{B}$
Step 4: Substitute the heat equations
Substituting the expressions for $Q_{A}$ and $Q_{B}$ :
$m_{A} \cdot c_{A} \cdot Δ T = 2 \cdot (m_{B} \cdot c_{B} \cdot Δ T)$
Step 5: Cancel out the common terms
Since $Δ T$ is the same for both liquids, we can cancel it from both sides:
$m_{A} \cdot c_{A} = 2 \cdot m_{B} \cdot c_{B}$
Step 6: Substitute the mass of liquid A
Now substitute $m_{A} = \frac{1}{2} m_{B}$ into the equation:
$(\frac{1}{2} m_{B}) \cdot c_{A} = 2 \cdot m_{B} \cdot c_{B}$
Step 7: Simplify the equation
Now, we can simplify this equation by dividing both sides by $m_{B}$ (assuming $m_{B} \neq 0$ ):
$\frac{1}{2} c_{A} = 2 c_{B}$
Step 8: Solve for the ratio of specific heats
Now, multiply both sides by 2 to isolate $c_{A}$ :
$c_{A} = 4 c_{B}$
Step 9: Find the ratio of specific heats
Now, we can find the ratio of the specific heat of A to that of B:
$\frac{c_{A}}{c_{B}} = 4$
Final Answer
The ratio of the specific heat of liquid A to that of liquid B is:
$\frac{c_{A}}{c_{B}} = 4 : 1$
---

Updated on:7/8/2024

On heating the viscosity of liquid sulphur are
Aincrases
Bdecreases
Cfirst increasea and then decreases
Dfirst decrease and the n increase
Vipin adds 3 litres of liquid A in 6 litres of liquid B and Mohit adds 8 litres of liquid A in 15 litres of liquid B. What is the ratio of the percentage of liquid B in the two mixtures?
A $26 : 25$
B $51 : 32$
C $46 : 45$
D $34 : 25$
Cooling graphs are drawn for three liquids a,b and c The specific heat is maximum for liquid
.
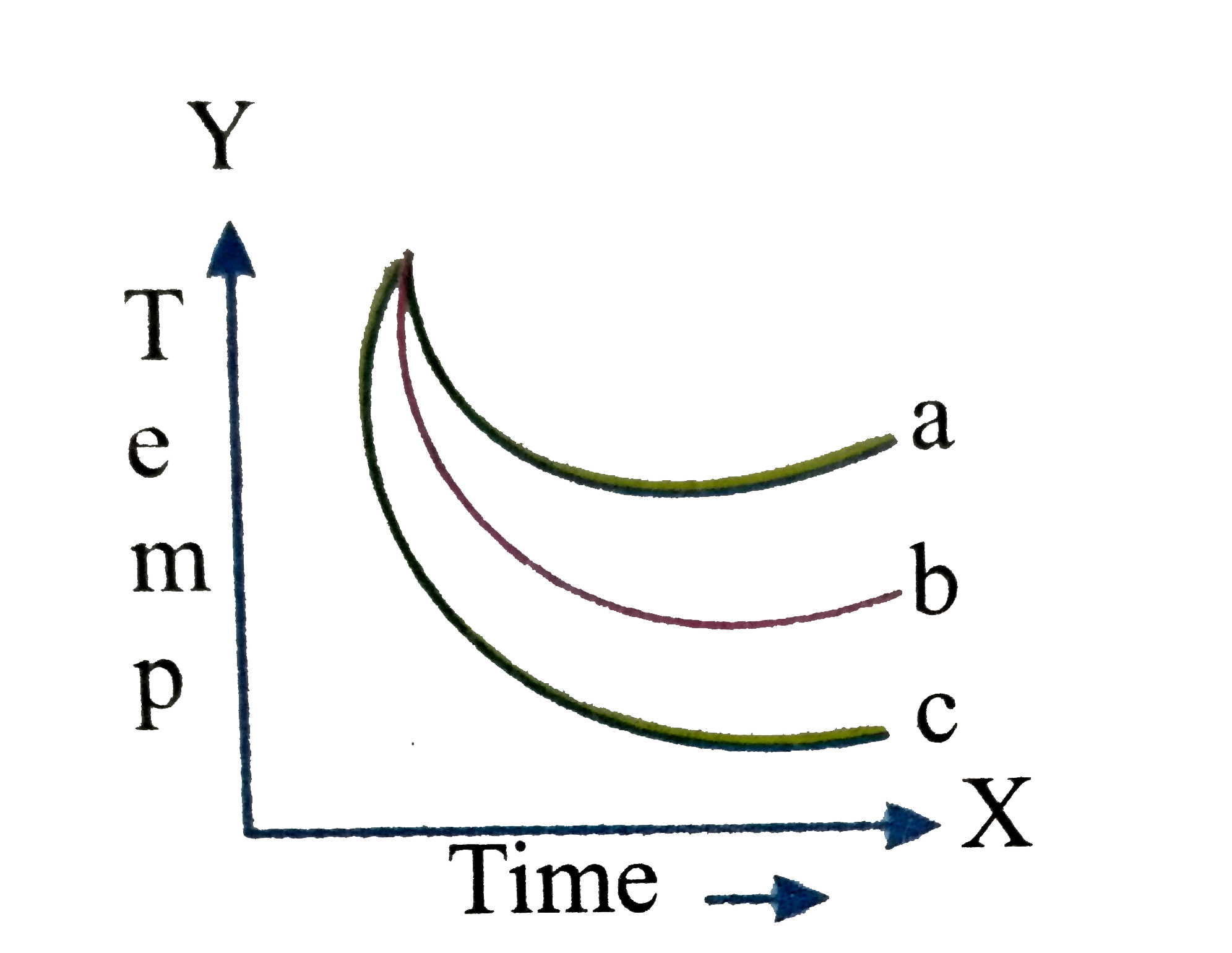A $a$
B $b$
C $c$
Dfor all the three a,b and c