In the adjoining figure, ΔABC is right angled at C and M is the mid-point of hypotenuse AB, If AC=32cm and BC=60cm, then find the length of CM.

A
32cm
B
30cm
C
17cm
D
34cm
Video Solution
Text Solution
The correct Answer is:D
Find AB using Pythagora's theorem and CM =12 AB.
|
Topper's Solved these Questions
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - SHORT ANSWER TYPE QUESTIONS
18 Videos
- COORDINATE GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - Level 3
9 Videos
- LINEAR EQUATIONS AND INEQUATIONSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LINEAR EQUATIONS AND INEQUATIONSEXERCISE - level 3
10 Videos
Similar Questions
Knowledge Check
In ΔABC,∠B is right angle and D is the mid-point of the side AC . If AB = 6 cm , BC = 8 cm , then the length of BD is
A4 cmB5 cmC8 cmD12 cmΔABC is right-angled at C. If AC=5cmandBC=12cm find the length of AB.
A17B7C13D14In a right angled ΔABC,∠C=90∘andCD is the perpendicular on hypotenuse AB if BC = 15 cm and AC=20cm then CD is equal to :
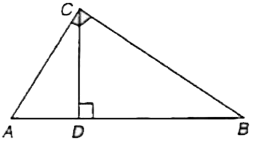 A18 cmB12 cmC17.5 cmDcan't be determined
A18 cmB12 cmC17.5 cmDcan't be determined
In the adjoining figure, AB=8cm,DM=6cmandBC=6cm. Find the length of DN

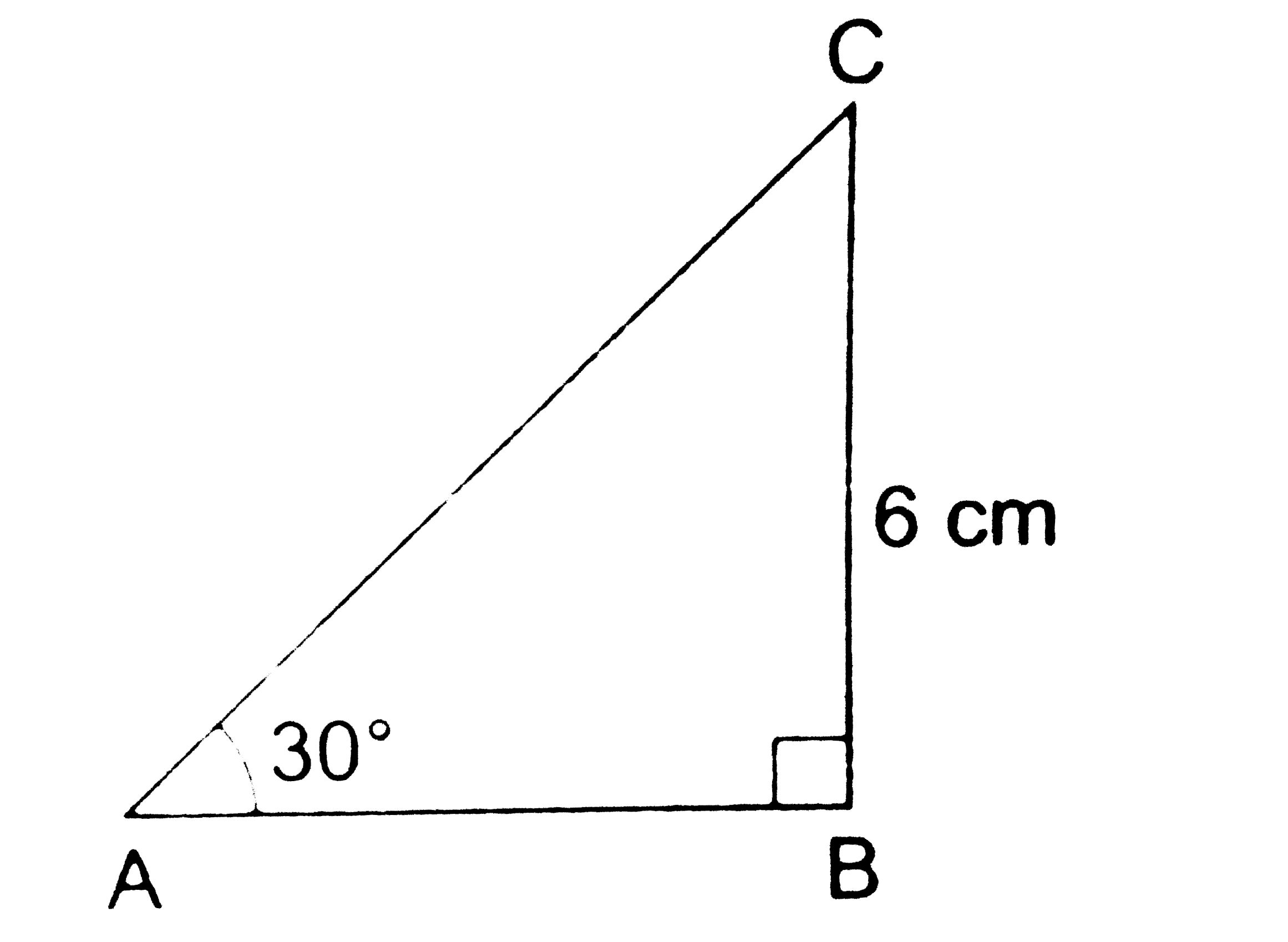
View SolutionIn the adjoining figure, ΔABC is right-angled at B. If ∠A=30∘ and AB=9cm, find (i)BC and (ii)AC.

View SolutionIn the adjoining figure, ΔABC is right-angled at B and ∠A=45∘ . If AC=3√2cm, find (i)BC, (ii)AB.

View SolutionIn ΔABC, ∠B=90∘. D is the midpoint of hypotenuse AC. If BD=4.5cm, then find the length of hypotenuse AC.
View Solution△ABC is a right angled at A and AD is the altitude to BC. If AB= 7 cm and AC = 24 cm. Find the ratio of AD is to AM if M is the mid-point of BC.
View Solution