A sloping plank is used to push goods onto a truck. Its length is 3 m and the end which touches the truck is at a height of 1.5 m. Calculate its M.A. If the effort applied is 25 N, what load can be pushed into the truck?
Step by step video & image solution for A sloping plank is used to push goods onto a truck. Its length is 3 m and the end which touches the truck is at a height of 1.5 m. Calculate its M.A. If the effort applied is 25 N, what load can be pushed into the truck? by Physics experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE MACHINESBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - SIMPLE MACHINESEXERCISE - Essay Type Questions
3 Videos
- SIMPLE MACHINESBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - SIMPLE MACHINESEXERCISE - Concept Application (Level - 1 )
44 Videos
- SIMPLE MACHINESBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - SIMPLE MACHINESEXERCISE - Very Short Answer Type Questions
30 Videos
- MODERN PHYSICSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MODERN PHYSICSEXERCISE - Level 3
5 Videos
- WAVES MOTION AND SOUND BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - WAVES MOTION AND SOUND EXERCISE - Level 3
10 Videos
Similar Questions
An inclined plane of length 2 m is used to load Maruti cars into a carrier truck. If the body of the truck is at a height of 1 m from the ground, find the effort required to load a car using the inclined plane. The unladen weight of a Maruti car is 600 kgwt (Take g=10ms−2)
View SolutionA plank of length 4 m is inclined to the ground such that its one end is resting on the ground and the other end is 1 m above ground level. Calculate the effort that has to be applied to push a load of 48 N up the plank.
View SolutionThe breadth of a room is twice its height and is half of its length. The volume of room is 512dm3. Its dimensions are :
View SolutionThe mechanical advantage of a machine is 5 and its efficiency is 75%. A load of 300 kgf is lifted with the help of this machine up to the height of 15 m. Calculate the effort needed for this purpose.
View SolutionA box of mass 4 kg is placed on a wooden plank of length 1.5m which is lying on the ground. The plank is lifted from one end along its length so that it becomes inclined. It is noted that when the vertical height of the top end of the plank from the ground becomes 0.5m, the box begins to slide. Find the coefficient of friction between the box and the plank.
View SolutionThe capacity of a cuboidal water tank is 1,00,000 litres. If its length is 5 m and breadth is 4 m, find its height.
View SolutionThe wooden plank of length 1 m and uniform cross section is hinged at one end to the bottom of a tank as shown in figure. The tank is filled with water up to a height of 0.5 m. The specific gravity of the plank is 0.5. Find the angle θ that the plank makes with the vertical in the equilibrium position. (Exclude the case θ=0)
 ,
,
View SolutionIf an inclined plane of length 2 m is used to lift a load of 20 N to a height of 1 m, find the effort required to lift the load to that heiht using inclined plane.
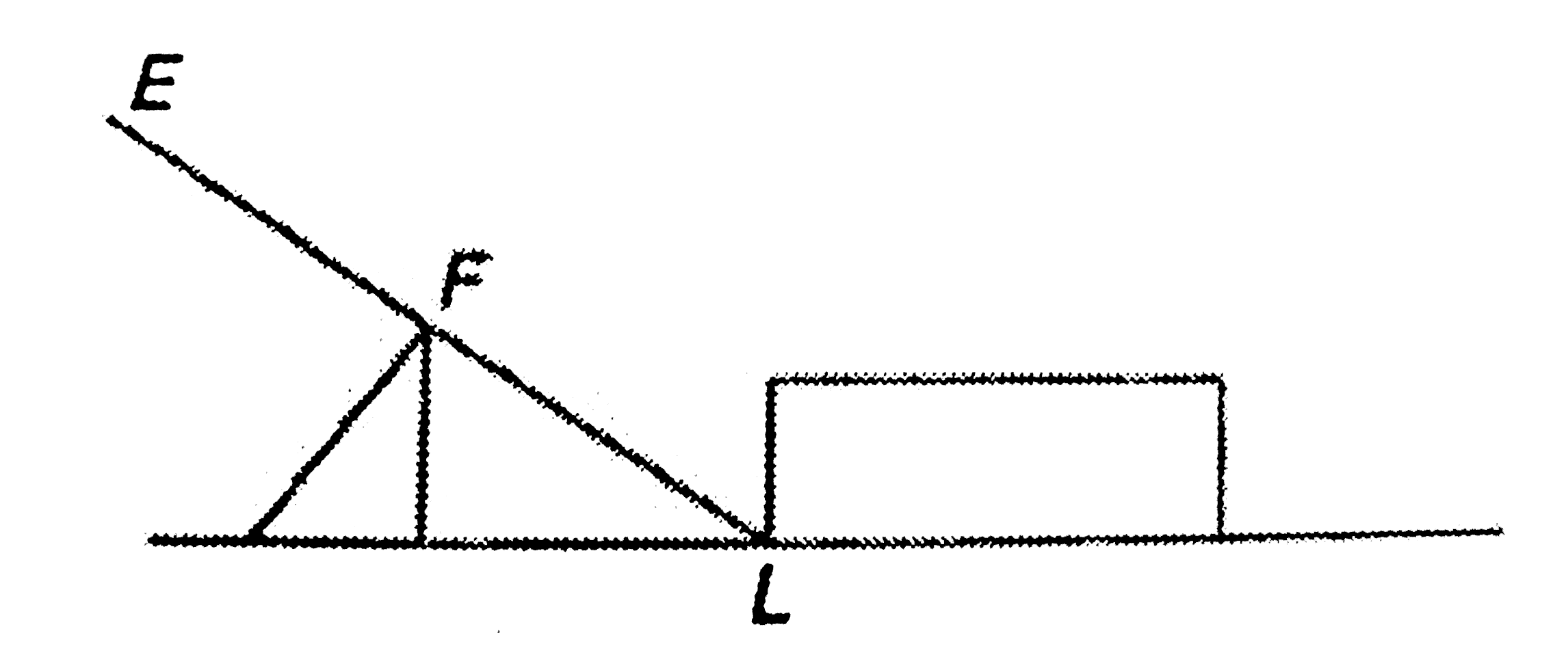
View SolutionIf an inclined plane of length 2 m is used to lift a load of 20 N to a height of 1 m, find the effort required to lift the load to that heiht using inclined plane.

View SolutionTwo thin circular disks of mass 2kg and radius 10 cm each are joined by a rigid massless rod of length 20 cm. the axis of the rod is along the perpendicular to the planes of the disk through their centres. This object is kept on a truck in such a way that the axis of the object is horizontal and perpendicular to the direction of the motion of the truck. Its friction with the floor of the truck is large enough so that the object can roll on the truck without slipping. Take x axis as the direction of motion of the truck and z-axis as the vertically upwards direction. if the truck has an acceleration of 9m/s2 Calculate:
(i) The force fo friction on each disk,
(ii) The magnitude and the direction of the frictional torque acting on each disk about the centre of mass O of the object. Express the torque in the vector form in terms of unit vectors ˆi,ˆjandˆk in the x,y, and z directions.
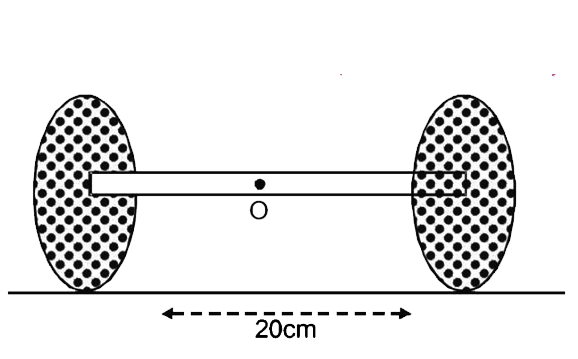
View Solution
