A hollow metallic sphere is heated. Explain in the type of change produced in its
(a) internal radius (b) external radius
(c) volume (d) mass
(e) density
(i) Take volumes of the body at t1∘C and t2∘C be V1andV2, respectively. Take the densities of the liquid at t1∘C and t2∘C as d1 and d2, respectively. Find the apparent loss in weight of the body in liquid at t1∘C and t2∘C.
W1−W2=V1d1g
and W1−W3=V2d2g
The volume coefficient of the solid body
=γ=ΔVV0ΔT=V2−V1V1(t2−t1)∘C−1
Convert V1andV2 in terms of W1,W2,g,d1andd2 Substitue it in above equation and obtain required solution.
(ii) d1(w1−w3)−d2(w1−w2)d2(t2−t1)(w1−w2)∘C−1
Topper's Solved these Questions
Similar Questions
Knowledge Check
A hollow metallic sphere of radius 0.1 m is charged to a potential of 5 V. The potential at its centre is
AinifiniteB5 VCzeroDcannot be determinedThe rate of change of volume of a sphere with respect to its radius when radius is 1 unit is :
A4πB2πCπDπ2.A hollow metallic sphere with external diameter 8 cm and internal diameter 4 cm is melted and moulded into a cone having base radius 4 cm. The height of the cone is
A12 cmB14 cmC15 cmD18 cm
A point charge is placed at the centre of a hollow conducting sphere of internal radius ' and outer radius '2r. The ratio of the surface charge density of the inner surface to that of the outer surface will be ___________ .
View SolutionFind the rate of change of volume of a sphere with respect to its radius when r=4cm
View Solution Figure shows charged hollow metal spheres (exceptX) each with internal radius a and external radius b Match each charged distribution with the corresponding E- field graph.
Figure shows charged hollow metal spheres (exceptX) each with internal radius a and external radius b Match each charged distribution with the corresponding E- field graph. 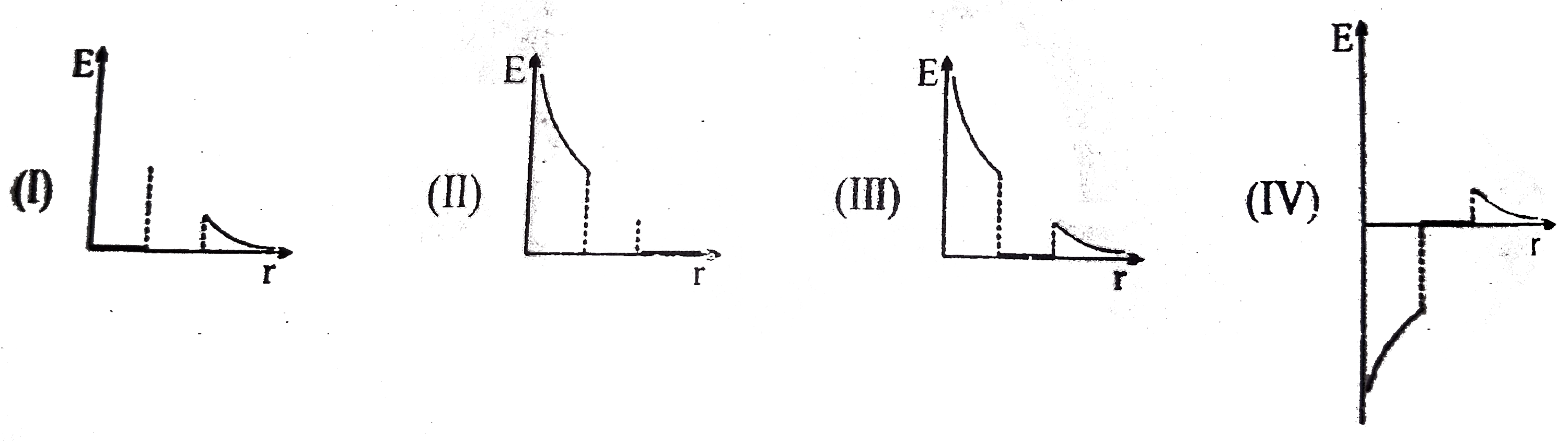
View SolutionA hollow metallic sphere of radius 5 cm is charged so that the potential on its surface is 10 V. Thepotential at the centre of the sphere is
View SolutionA cylinder has the same height as the radius of its base. A hollow sphere has the same outer radius as that of the base of the cylinder while the inner radius is half of the outer radius. Find the ratio of the volumes of the cylinder to the hollow sphere.
View Solution
