A, B , C and D are four transparent sheets of equal thickness and made of material of refractive indices μA,μB,μC,andμD. If a light ray propagates through them as shown in the figure, compare their refractive indices and also find if any of them have the same refractive index.

Let us represent angles of incidence and angles of refraction in A, B , C , D as iA,iB,ic,iD,rA,rB,rCandrD, respectively.
rB<iA⇒μB>μA
rC>iB⇒μB>μC
rC=rA⇒μC=μA
rD<ic⇒μD>μC
rB<rD⇒μB>μD
as such mA=μC<μD<μB
Topper's Solved these Questions
Similar Questions
Knowledge Check
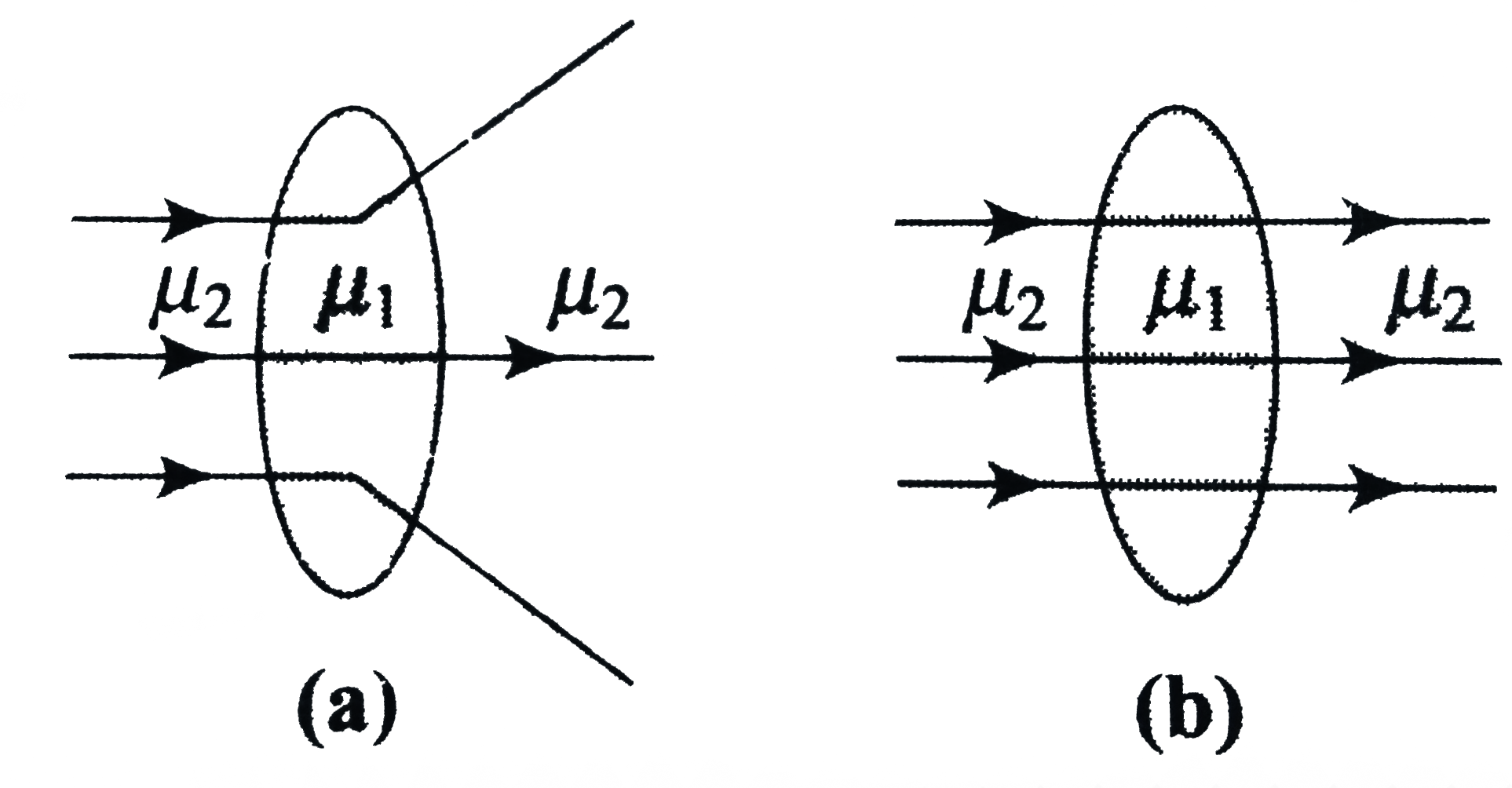
If the behaviour of light rays is as shown in the figure. The relation between refractive indices μ,μ1 "and" μ2 is
 Aμ>μ2>μ1Bμ<μ2<μ1Cμ<μ2,μ=μ1Dμ2<μ1,μ=μ2
Aμ>μ2>μ1Bμ<μ2<μ1Cμ<μ2,μ=μ1Dμ2<μ1,μ=μ2The relation between refractive indices u,μ1,μ2. if the behaviour of light ray is as shown in figure
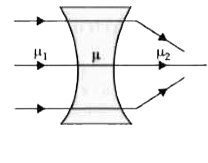
 Aμ>μ1>μ2Bμ<μ2<μ1Cμ<μ2,μ=μ1Dμ2<μ1,μ=μ2
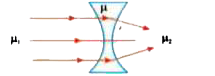
Aμ>μ1>μ2Bμ<μ2<μ1Cμ<μ2,μ=μ1Dμ2<μ1,μ=μ2A convex lens made up of material of refractive index μ1, is immersed in a medium of refractive index μ2 as shown in the figure. The relation between μ1 and μ2 is
 Aμ1<μ2Bμ1>μ2Cμ1=μ2Dμ1=√μ2
Aμ1<μ2Bμ1>μ2Cμ1=μ2Dμ1=√μ2
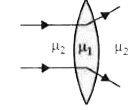
A transparent cube of side d, made of a material of refractive index μ2 , is immersed in a liquid of refractive index μ1(μ1<μ2). . A ray is incident on the face AV at an angle θ (shown in the figure). Total internal refraction takes place at point E on the face BC. Then must satisfy:
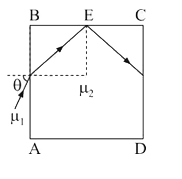
View SolutionA transparent cube of side d, made of a material of refractive index μ2 , is immersed in a liquid of refractive index μ1(μ1<μ2). . A ray is incident on the face AV at an angle θ (shown in the figure). Total internal refraction takes place at point E on the face BC. Then must satisfy:

View SolutionA transparent cube of side d, made of a material of refractive index μ2 , is immersed in a liquid of refractive index μ1(μ1<μ2). . A ray is incident on the face AV at an angle θ (shown in the figure). Total internal refraction takes place at point E on the face BC. Then must satisfy:

View SolutionTwo optical media of refractive indices μ1 and μ2 contain x and y waves of same colour in the same thickness. Their refractive indices ratio is equal to
View SolutionTwo optical media of refractive indices μ1 and μ2 contain x and y waves of same colour in the same thickness. Their refractive indices ratio is equal to
View Solution