P amount of lateral pressure is applied on either sides of a cuboidal dough horizontally. The length of the dough is reduced to half resulting change only in the height, then fmd the pressure applied by the dough at the bottom of it.
The correct Answer is:2P1
P1=mgl×b
P2=mgl2×b
P2=2P1
Topper's Solved these Questions
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - Force and Pressure EXERCISE - CROSSWOARD1videos
Force and Pressure
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - Force and Pressure EXERCISE - Examples6videos
Force and Pressure
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - Force and Pressure EXERCISE - CROSSWORD1videos
Force and Pressure
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - ENVIRONMENT- AN ETERNAL GIFT TO MANKINDEXERCISE - Crossword1videos
ENVIRONMENT- AN ETERNAL GIFT TO MANKIND
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LIGHTEXERCISE - ASSESSMENT TEST (CROSS WORD )11videos
LIGHT
Similar Questions
P amount of lateral pressure is applied on either sides of a cuboidal dough horizontally. The length of the dough is reduced to half resulting change only in the height, then fmd the pressure applied by the dough at the bottom of it.
View SolutionA unifrom pressure P is exerted P is exerted on all sides of a solid cube at temperature be raised in order to bring cubic volume back to what it had been before the pressure was applied (Xcubicacl expansivity of the material of the cude =α and the bulk modulus of elasticity is β)
⎡⎢ ⎢⎣Hint:Pchange in volumeoriginalVt=V0(1+αt)⎤⎥ ⎥⎦View Solution
Knowledge Check
- Question 1 - Select One
Some liquid is filled in a cylindrical vessel of radius R. Let F1 be the force applied by the liquid on the bottom of the cylinder. Now the same liquid is poured into a vessel of uniform square cross-section of side R. Let F2 be the force applied by the liquid on the bottom of this new vessel. (Neglect atmosphere pressure). Then
AF1=πF2BF1=F2πCF1=√πF2DF1=F2 - Question 2 - Select One or More

Artificial satellites go round the earth in their respective orbits. Astronauts are able to float in side the satellite. Inside space of the satellite could be treated as gravity free space. If a beaker filled with a liquid upto height h having a small hole in the bottom is placed in such a satellite, you will wonder te liquid does not come out of the hole. You have to squeeze or force the liquid to come out. suppose a constant pressure p is applied on the liquid through piston to force it out through the hole. Out side pressure could be neglected in comparison with p Cross-sectional area of beaker is too greater than that of hole (A>>a)Avelocity with which liquid comes out of the hole is √pρBvelocity with which liquid comes out of the hole is √2pρCTime taken to empty the beaker is Aha√ρ2pDTime taken to empty the beaker is Aha√2ρp - Question 3 - Select One
A container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The total pressure with cylinder, at the bottom of the container isAp0+(6L+H)4dgBp0+(L+6H)4dgCp0+(L+3H)4dgDp0+(L+2H)4dg
The change in the magnitude of the volume of an ideal gas when a small additional pressure ΔP is applied at a constant temperature, is the same as the change when the temperature is reduced by a small quantity ΔT at constant pressure. The initial temperature and pressure of the gas were 300 K and 2 atm. respectively. If |ΔT|=C|ΔP| then value of C in (K/atm) is __________.
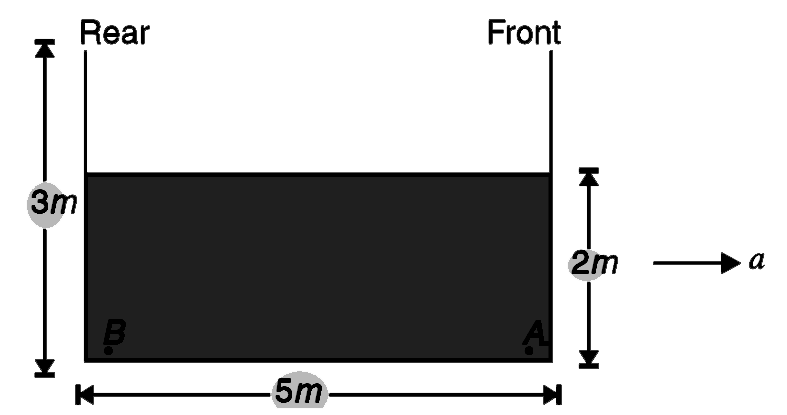
View SolutionAn open rectangular tank 5mxx4mxx3m in dimension is containing water up to a height of 2m the tank is accelerated horizontally along the longer side. Assuming water to be and ideal liquid find-
(a) the maximum acceleration with which the tank can be moved so that water does not fall from the rear side.
(b) the gauge pressure at the bottom of the front and back of the tank (points A and B) if the tank is closed at the top and is then acclerated horizontally at 9m/s2. Assume that the top cover has a small hole at the right side of the tank so taht pressure of air inside the tank is maintained at atmospheric pressure. Gauge pressure at a point is difference in absolute pressure at the point and atmospheric pressure.
 View Solution
View SolutionLength of a horizontal arm of U-tube is L and ends of both the vertical arms are open to atompsheric pressure P0, A liquid of density ρ is poured in the tube such that liquid just fills the horizontal part of the tube as shown in figure . Now one end of the opened ends is sealed and the tube is then rotated about a vertical axis passing through the other vertical arm with angular speed ω0. if length of each vertical arm is a and in the sealed end liquid rises to a height y, find pressure in the sealed tube during rotation.
View SolutionA uniform pressure P is exerted on all sides of a solid cube at temperature t ∘C. By what amount should the temperature of the cube be raised in order to bring its volume back to the value it had before the pressure was applied? The coefficient of volume expansion of cube is α and the bulk modulus is K.
View SolutionOut of the three stes of matter, only the gases have most of the physical properties common. They neither have definite shapes nor volumes. Upon mixing they form hoogeneous mixture irespective of their nature and can also be compressed on applying pressure. In addition to these, the gases obey different gas laws such as Noyle's Law, Charles's Law, Dalton's Law of partial pressures, Graham's Law of diffusion etc. Based upon these laws, ideal gas equation PV=nRT has been derived.
When the produce of pressure and volume is plotted against pressure for a given amount of a gas, the obtained isView Solution

