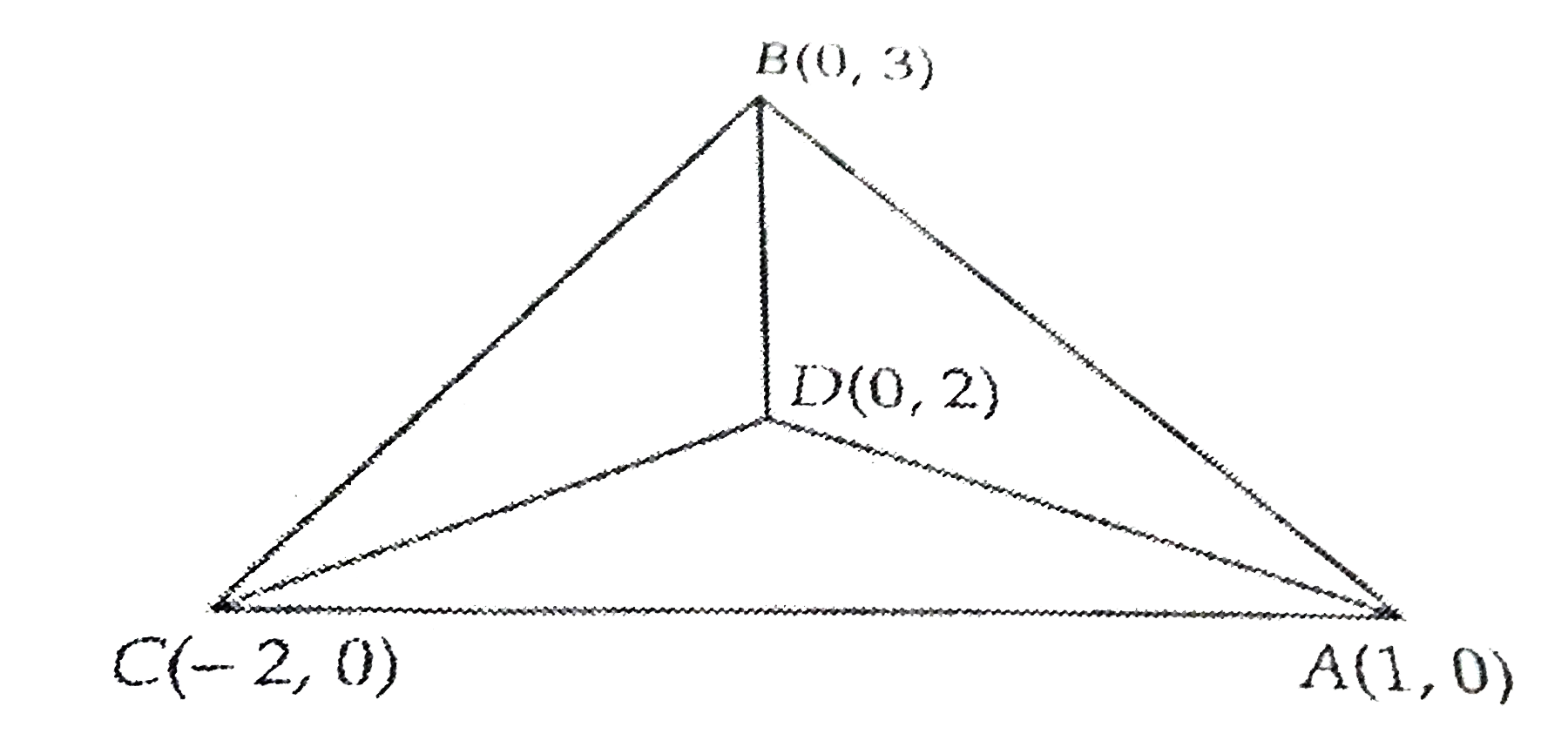
Statement-1: The quadrilaterial whoe vertices (in order) are A(1,0), B(0,3) , C(-2,0) and D(0,2) cannot be convex.
Statement-2: A quadriilateral ABCD ( in oder is) is convex iff when any diagonla is taken then the remaining vertices must be on the opposite sides of it.
Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1
Statement-1 is True, Statement-2 is True, Statement-2 not a correct explanation for Statement-1
Statement-1 is True, Statement-2 is False.
Statement-1 is False, Statement-2 is True
The correct Answer is:A
Statement-2 is correct the because ifn one angle, say D of the equadrilaterial ABCD which is not convex is more thant 180∘, then B and D lie on the same side of the diagonal AC.
Statement-2 is true. Also, statement-2 is a correct explanation for statement-1
Topper's Solved these Questions
- CARTESIAN CO-ORDINATE SYSTEM BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN CO-ORDINATE SYSTEM EXERCISE - Exercise
29 Videos
- CARTESIAN CO-ORDINATE SYSTEM BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN CO-ORDINATE SYSTEM EXERCISE - Section I - Solved Mcqs
29 Videos
- BINOMIAL THEOREM AND ITS APPLCIATIONS BOOK - OBJECTIVE RD SHARMACHAPTER - BINOMIAL THEOREM AND ITS APPLCIATIONS EXERCISE - Chapter Test
60 Videos
- CONIC SECTIONSBOOK - OBJECTIVE RD SHARMACHAPTER - CONIC SECTIONSEXERCISE - Section I - Solved Mcqs
1 Videos
Similar Questions
Knowledge Check
The area of the triangle whose vertices are A(1,2−1) B (3,1,4) and C (0,2,3)
A√1762sp unitB8 sq unitC√1862 sq unitDNone of these
Find the area of a quadrilateral ABCD having vertices at A(l, 2), B(1, 0), C(4,0) and D(4,4).
View SolutionThe vertices of a triangle ABC are A(0,0) , B(2,-1) and C(9,2). Evaluate cosB
View Solutionfind the area of the quadrilateral ABCD with vertices A(−2,0),B(0,4),C(4,−2),D(2,2)
View SolutionThe vertices of a triangle ABC are A(0,0),B(2,−1)andC(9,2), find cosB.
View SolutionThe points A(3,1) , B (12,-2) and C(0,2) cannot be vertices of a triangle.
View SolutionFind the equation of the sides of ΔABC whose vertices are A(2,−3), B(0,1) and C(4,2).
View SolutionThe vertices of quadrilateral ABCD are A(5,-1) B(8,3), C(4,0) and D(1,-4). Prove that ABCD is a rhombus.
View Solution
