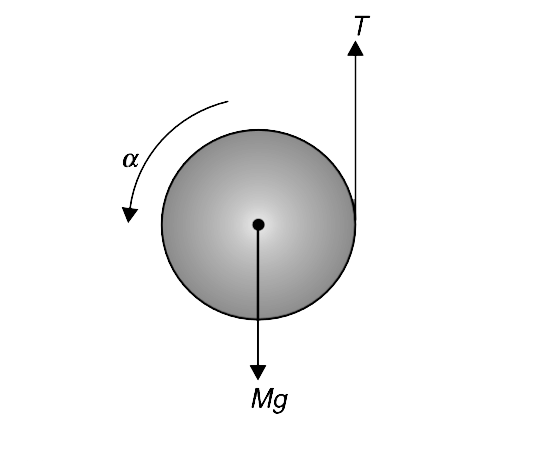
A string is wrapped around a cylinder of mass M and radius R(=2√2m).The string is pulled vertically upward to prevent the centre of mass from falling as the cylinder unwinds the string.Find the length of the string unwound when the cylinder has reached a speed ω(=5rad/s).(g=10ms2)
Step by step video & image solution for A string is wrapped around a cylinder of mass M and radius R(=2sqrt(2)m).The string is pulled vertically upward to prevent the centre of mass from falling as the cylinder unwinds the string.Find the length of the string unwound when the cylinder has reached a speed omega(=5rad/s).(g=10m/s^(2)) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
A string is wrapped around a cylinder of mass M and radius r. The string is pulled vertically upward to prevent the center of mass from falling as the cylinder unwinds the string. (a) What is the tension in the string? B) How much work has been done on the cylinder once it has reached an angular speed ω? c) what is the length of string unwound in the time its acquires angular speed ω?
View SolutionA string is wrapped around a cylinder of mass M and radius R. The string is pulled vertically upward to prevent the centre of mass from falling as the string unwinds. Assume that the cylinder remains horizontal throughout and the thread does not slip. Find the length of the string unwound when the cylinder has reached an angular speed ω.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A string is wrapped around a cylinder of mass M and radius R. The string is pulled vertically upwards to prevent the centre of mass from falling as the cylinder unwinds the string. The tension in the string is
AMg6BMg3CMg2D2Mg3 - Question 2 - Select One
A string is wrapped around a cylinder of mass M and radius R. The string is pulled vertically upwards to prevent the centre of mass from falling as the cylinder unwinds the string. The tension in the string is
A2Mg/3BMg/2CMg/3DMg/6 - Question 3 - Select One
A string of negligible mass is wrapped on a cylindrical pulley of mass M and radius R. The other end of string is tied to a bucket of mass m. If the pulley rotates about a horizontal axis then the tension in the string is :
AmgB(M+m)gCMmg(M+2m)D2mg(M+2m)
A string is warapped around a cylinder of mass m and radius r. The string is also connected to a block of same mass m with the help of another pulley as shown in figure. The angular acceleration of the cylinder is ( friction is sufficient for rolling ) ( all pulleys are ideal)
 View Solution
View SolutionA string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
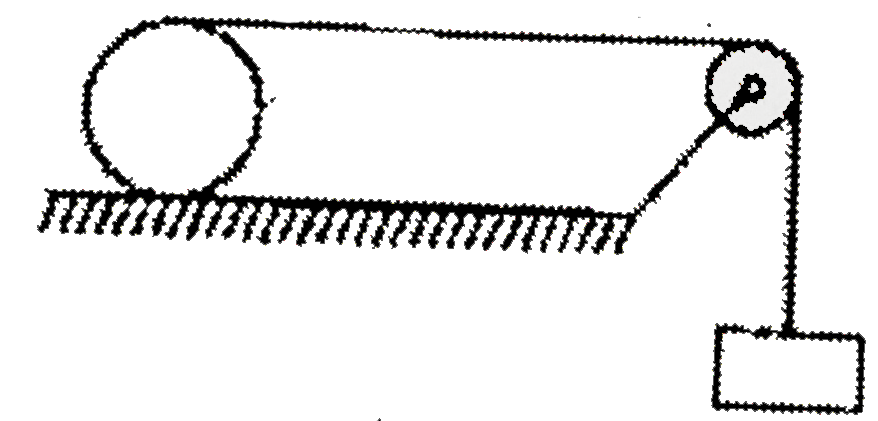
Velocity of point of contact 'of cylinder at this moment is:View SolutionA string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
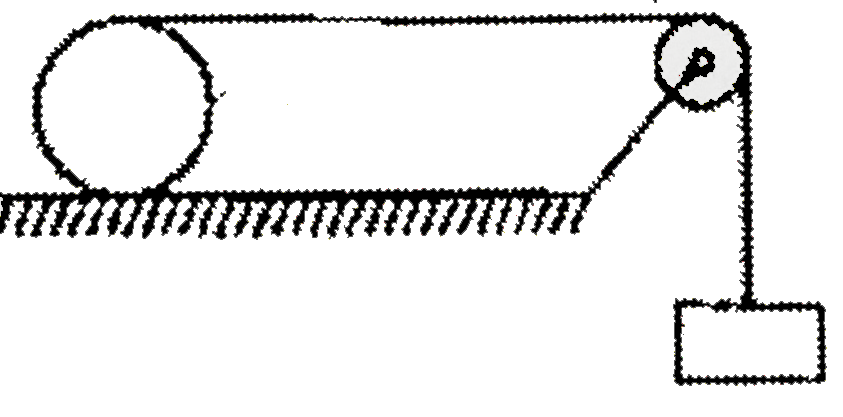
Acceleration of cylinder is:View SolutionA string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
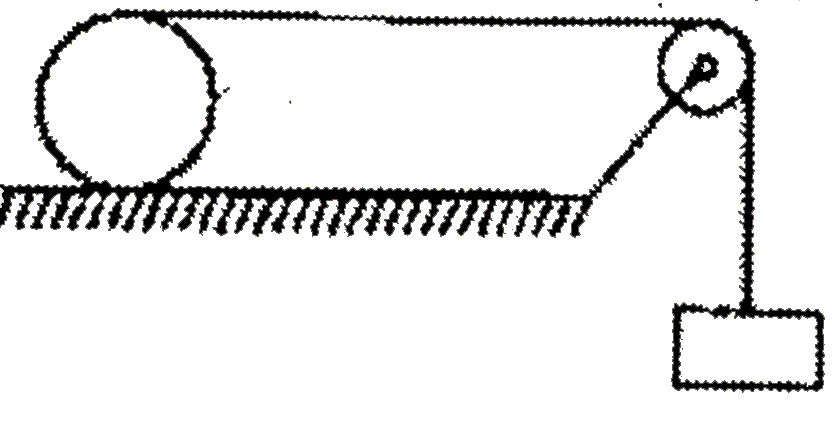
Acceleration of hanging mass is:View SolutionA string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
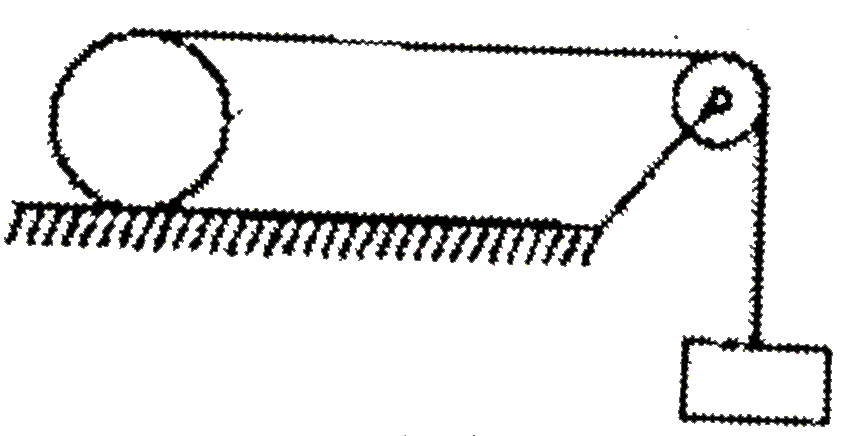
Velocity of hanging block at this moment is: is:View Solution
