মনে করাে, সব স্বাভাবিক সংখ্যার সেট N এবং a∈N , যদি aN={ax:x∈N} এবং pN∩qN=rN, যেখানে p,q,r∈N হয়, তবে দেখাও যে , p,q -এর লসাগু হবে r
Step by step video & image solution for মনে করাে, সব স্বাভাবিক সংখ্যার সেট N এবং a in N , যদি aN = {ax : x in N} এবং pNnnqN=rN, যেখানে p,q, r in N হয়, তবে দেখাও যে , p,q -এর লসাগু হবে r by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
চারটি পদবিশিষ্ট কোনাে সেটের উপসেটগুলির সংখ্যা হল-
View Solutionসঠিক উত্তরটি নির্বাচন করো
x=P13+P−13(P≠0) হলে (Px3−3Px−P2) এর মান হবে -
View SolutionP={a,b,c,d,e} এবং Q={a,e,i,o,u} হলে প্রমান কর যে , P⊂P∪Q
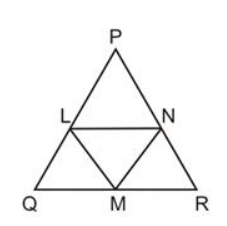
View SolutionIn ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.
View SolutionIf p+q=1, then show that n∑r=0r2^nCrprqn−r=npq+n2p2.
View SolutionIf nC0,nC1,...,nCn denote the binomial coefficients in the expansion of (1+x)nandp+q=1 , then n∑r=0r.nCrprqn−r=
View SolutionIf (n)C0,(n)C1,(n)C2,....,(n)Cn, denote the binomial coefficients in the expansion of (1+x)nandp+q=1 n∑r=0r2 nCrprqn−r= .
View Solutionমনে করো, A একটি 2×2ক্রমেরম্যাট্রিক্স,এবংA^2=0 (যেখানে0একটিশূন্যম্যাট্রিক্স,)I 2times2ক্রমেরএককম্যাট্রিক্সতবে−যদিA!=০এবংA= [[a,b],[c,d]] , ad-bc=0এবংA^2-(a+d)A+(ad-bc)I =0হয়,তবেa+d এর মান হবে-
View SolutionIf a:b=c:d=e:f then (pa+qc+re):(pb+qd+rf) is equal to
View SolutionIf p+q=1, then show that n∑r=0r2^nCrprqn−r=npq+n2p2.
View SolutionIn ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.
View SolutionIn ΔABC and ΔPQR, AB=PQ, BC=QR and CB and RQ are extended to X and Y respectively and ∠ABX=∠PQY. Prove that ABC≅ PQR.
View SolutionIn triangle PQR, if PQ=RQ and L, M and N are the mid-points of the sides PQ, QR and RP respectively. Prove that LN=MN.
View SolutionIn A PQR, if PQ=QR and L, M and N are the mid-points of the sides PQ, PR and RP respectively. Prove that LN=MN
View SolutionIf P={5,6,8,10,12,},Q={0,3,6,9,12,15,8}andR={0,1,2,3,….10}
n(P∩Q),n(Q∩R)andn(P∩R)
View Solution
