0 ° < θ < 360 °என்ற இடைவெளியில் கீழ்கண்ட சமன்பாடுகளுக்கு சரியான தீர்வுகளை காண்க: cos2x=1-3sinx
Step by step video & image solution for 0 ° < θ < 360 °என்ற இடைவெளியில் கீழ்கண்ட சமன்பாடுகளுக்கு சரியான தீர்வுகளை காண்க: cos2x=1-3sinx by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A=[ex−2e7+xe2+xe2x+3] என்பது ஒரு பூஜ்ஜியக்கோவை அணி எனில், x-ன் மதிப்பு :
View Solutionlimx→2x−2x2−x−2

View SolutionIf y=2cosx+3sinx−cos2x, then d2ydx2+y=
View SolutionLet three sets be defined as
A={x∣cos2x+cosx+1=0}
B={x∣cos2x+3sinx=2}
( c) {x∣secx+tanx=cosx}
The number of elements in A∩B∩C is
View SolutionLet f(θ)=sinθ⋅sin(60∘+θ)sin(60∘−θ) then 1.) The Minimum of f(θ) is ' − 1 ' 2.) The Maximum of f(θ) is 14 , 3.) The Range of f(θ) is [ − 13, 14 ] , 4.) The Range of f(θ) is [ − 14, 14 ]
View SolutionIf y √1−cos2x1+cos2x then dydx=0
View Solutiona+1a=6எனில்,a^3 + 1/a^3 இன் மதிப்பு காண்க.
View Solutionபின்வரும் வகையீடுகளைப் பொருத்துக
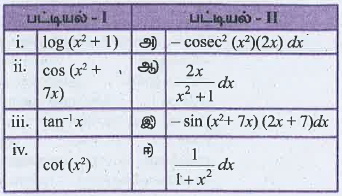 . சரியான பொருத்தமானது
. சரியான பொருத்தமானது
View SolutionSolve 2cos2x+3sinx=0.
View Solution(lim)x→0cos2x−1cosx−1
View SolutionEvaluate the following limit: (lim)x→01−cos2xcos2x−cos8x
View SolutionLet three sets be defined as
A={x∣cos2x+cosx+1=0}
B={x∣cos2x+3sinx=2}
C={x∣secx+tanx=cosx}
The number of elements in A∩B∩C is
View SolutionIf 3cosx+2cos3x=cosy, 3sinx+2sin3x=siny, then cos2x equals
View SolutionProve: sin θ(1 + tan θ) + cos θ(1 + cot θ) = (sec θ + cosec θ) .
View Solution(1 + cot2 θ) (1 – cos θ) (1 + cos θ) = …………………. (a) tan2 θ – sec2 θ (b) sin2 θ – cos2 θ (c) sec2 θ – tan2 θ (d) cos2 θ – sin2 θ
View Solution