(5, 4, 2) என்ற புள்ளியிலிருந்து x+12=y−33=z−1−1 என்ற நோ்க்கோட்டிற்கு வரையப்படும் செங்குத்துக் கோட்டின் அடியைக் காண்க. மேலும், இச்செங்குத்துக் கோட்டின் சமன்பாட்டைக் காண்க.
Step by step video & image solution for (5, 4, 2) என்ற புள்ளியிலிருந்து frac{x+1}{2}=frac{y-3}{3}=frac{z-1}{-1} என்ற நோ்க்கோட்டிற்கு வரையப்படும் செங்குத்துக் கோட்டின் அடியைக் காண்க. மேலும், இச்செங்குத்துக் கோட்டின் சமன்பாட்டைக் காண்க. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
→a மற்றும் →b என்பன இணைவெக்டர்கள் எனில், [→a→b→c]-ன் மதிப்பு காண்க.
06:14View Solutionநேரியல் தோராய மதிப்பீட்டு முறையில் பின்வருவனவற்றின் தோராய மதிப்புகளைக் காண்க. (123)23
08:09View Solutionx−12=y+13=z−14 மற்றும் x−31=y−m2=z என்ற கோடுகள் ஒரு புள்ளியில் வெட்டிக் கொள்ளும் எனில், m-ன் மதிப்பைக் காண்க.
10:23View Solution(2, 3, 6) என்ற புள்ளி வழிச் செல்வதும் x−12=y+13=z−31 மற்றும் x+32=y−3−5=z+1−3 என்ற கோடுகளுக்கு இணையானதுமான தளத்தின் துணையலகு அல்லாத வெக்டர் சமன்பாடு மற்றும் கார்டீசியன் சமன்பாடுகளைக் காண்க.
04:35View Solutionx−21=y−31=z−43 மற்றும் x−1−3=y−42=z−51 என்ற கோடுகள் ஒரு தளத்தில் அமையும் எனக்காட்டுக. மேலும், இக்கோடுகள் அமையும் தளத்தினைக் காண்க.
03:37View Solutionx−23=y+1−2,z=2 மற்றும் x−11=2y+33,z+52 என்ற கோடுகளுக்கு இடைப்பட்ட கோணம்.
02:55View Solutionநேர்க்கோடுகள் x−32=y+54=z−1−13 மற்றும் x+13=y−45=z+22என்பது
10:35View Solutionநேர்க்கோடுகள் x+22=y−3=z−14 மற்றும் x−3a=y−14=z−7a செங்குத்து எனில், (→a) -ன் மதிப்பு
05:58View Solutionபொருத்துக: கோடுகளுக்கு x−14=2−y6=z−412,x−3−2=y−33=5−z6
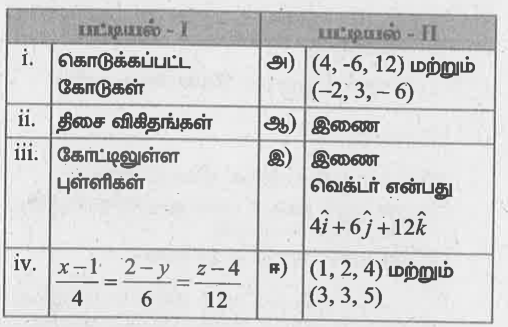 09:28View Solution
09:28View Solutionx−13=y+12=z−15 மற்றும் x−24=y−13=z+1−2 வெட்டுவதில்லை எனக்காட்டுக.
10:37View SolutionSolve (use matrix method): 2x−3y+3z=10, 1x+1y+1z=10, 3x−1y+2z=13.
10:37View SolutionSolve the system of equations. 6x+9y−20z=2 , 4x−6y+5z=1 and 2x+3y+10z=4
10:37View SolutionSolve the system of equations. 4x−6y+5z=1, 2x+3y+10z=4 and 6x+9y−20z=2
02:30View SolutionSolve the system of equations. 2x+3y+10z=4 , 4x−6y+5z=1 and 6x+9y−20z=2
02:15View Solutionনীচের সমীকরণটি সমাধান করো : x2−25=x3+14
10:42View SolutionSolve the following linear equations.
x2−15=x3+1411:29View Solution

