Sixteen players P1,P2,P3…..,P16 play in tournament. If they grouped into eight pair then the probability that P4 and P9 are in different groups, is equal to
Step by step video & image solution for Sixteen players P_(1),P_(2),P_(3)….., P_(16) play in tournament. If they grouped into eight pair then the probability that P_(4) and P_(9) are in different groups, is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Sixteen players S1,S2,...,S16 play in a tournament. They are divided into eight pairs at random. From each pair a winner is decided on the basis of a game played between the two players of the pair. Assume that all the players are of equal strength.Find the probability that the player S1 is among the eight winners.
View SolutionSixteen players S1,S2,…,S16 play in a tournament. They are divided into eight pairs at random. From each pair a winner is decided on the basis of a game played between the two players decided to the basis of a game played between the two players of the pair. Assume that all the players are of equal strength.
(a) Find the prabability that the player S1 is among the eight winners.
(b) Find the probability that exactly one of the two players S1andS2 is among the eight winners.
View Solution
Knowledge Check
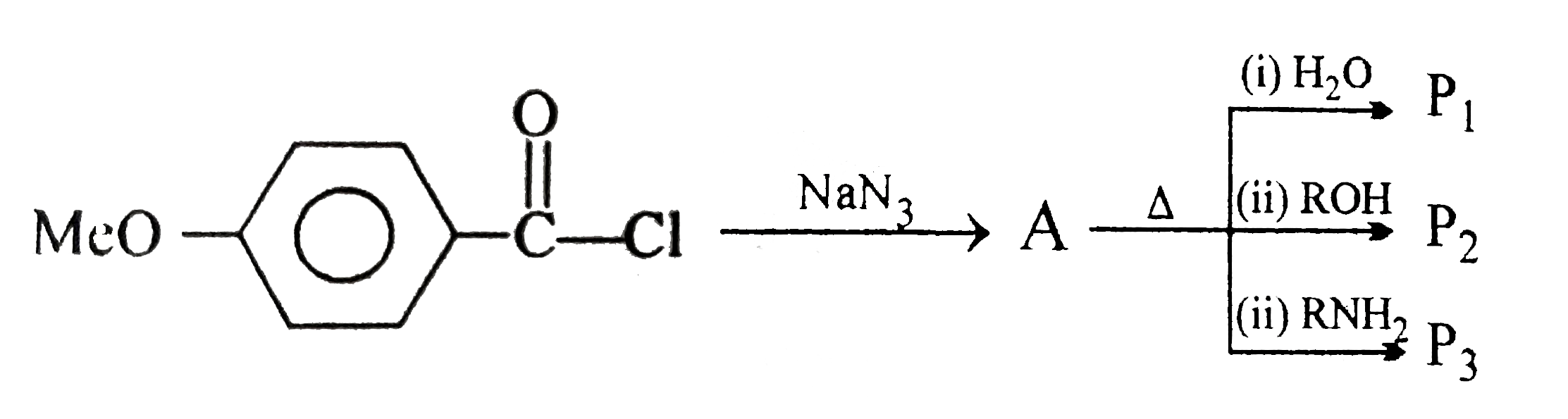
P1,P2,P3,are:A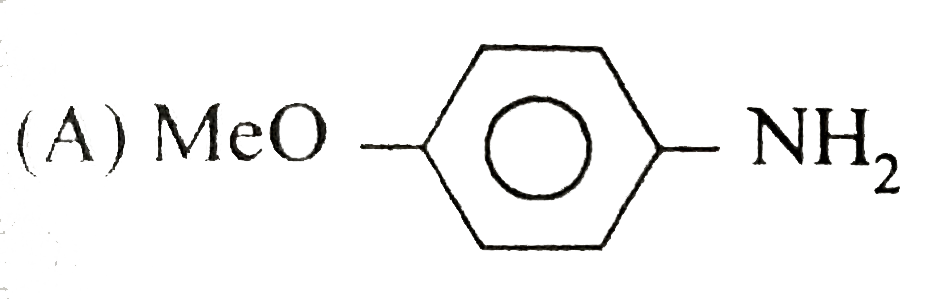 B
B C
C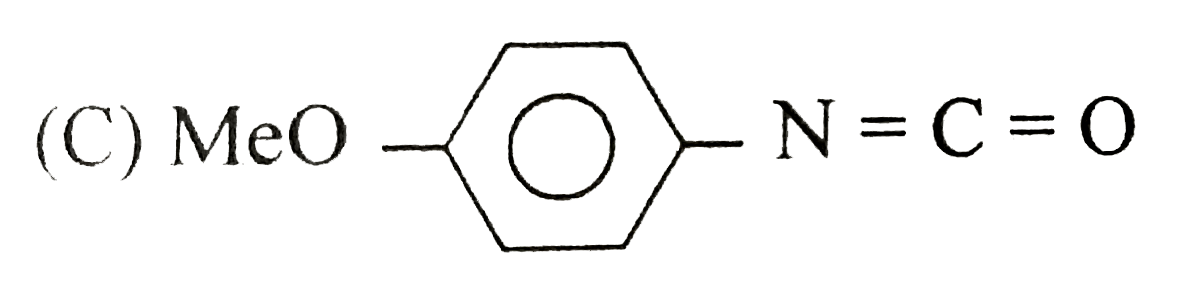 D
D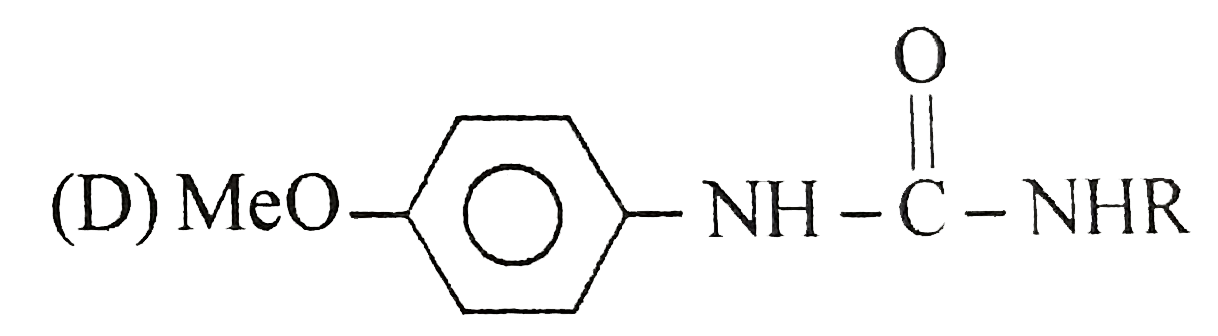
Sixteen players S1, S2, S3,…,S16 play in a tournament. Number of ways in which they can be grouped into eight pairs so that S1 and S2 are in different groups, is equal to
A(14)!26⋅6!B(15)!27⋅7!C(14)!27⋅6!D(14)!26⋅7!16 players P1,P2,P3,….P16 take part in a tennis tournament. Lower suffix player is better than any higher suffix player. These players are to be divided into 4 groups each comprising of 4 players and the best from each group is selected to semifinals.
Q. Number of ways in which they can be divided into 4 equal groups if the players P1,P2,P3 and P4 are in different groups, is:A(11)!216B(12)!(3!)4C(12)!(3!)4(4!)D(11)!(3!)4
Sixteen players S1,S2,…..S16 play in a tournament. They are divided into eight pairs at random from each pair a winner is decided on the basis of a game played between the two players of the pair. Assume that all the players are of equal strength.
(i) Find the probability that the player S1 is among the eight winners.
(ii) Find the probability that exactly one of the two playersS1 and S2 is among the eight winners.
View Solution8n players P1,P2,P3,....,P8n play a knock out tournament. It is known that all the players are of equal strngth. The tournat random is held in three rounds where the players are paired at random in each rouns. If it is given that P1 wins in the third round. Find the probability than P2 loses in the second round.
View Solution8n players P1,P2,P3……..P8n play a knock out tournament. It is known that all the players are of equal strength. The tournament is held in 3 where the players are paired at random in each round. If it is given that P1 wins in the third round. Find the probability that P2 looses in the second round.
View SolutionEight players P1,P2,P3,...........P8, play a knock out tournament. It is known that whenever the players PiandPj, play, the player Pi will win if i<j. Assuming that the players are paired at random in each round, what is the probability that the players P4, reaches the final ?
View Solution16 players P1,P2,P3,….P16 take part in a tennis tournament. Lower suffix player is better than any higher suffix player. These players are to be divided into 4 groups each comprising of 4 players and the best from each group is selected to semifinals.
Q. Number of ways in which these 16 players can be divided into four equal groups, such that when the best player is selected from each group P6 in one among them is (k)12!(4!)3 the value of k is
View Solution
