Question

Let $PQR$ be a triangle of area $\Delta$ with $a=2,b=\frac{7}{2}\text{and}c=\frac{5}{2},$ where $a,b\text{and}c$ are the lengths of the sides of the triangle opposite to the angles at $P,Q\text{and}R$ respectively. Then $\frac{2\sin P-\sin 2P}{2\sin P+\sin 2P}$ equals

Options

A. `(3)/(4Delta)`
B. `(45)/(4Delta)`
C. `((3)/(4Delta))^(2)`
D. `((45)/(4Delta))^(5)`

Answer

C

Explanation

If `DeltaABC` has sides a,b,c,

Then `tan(A//2)=sqrt(((s-b)(s-a))/(s(s-a)))`
Where `s=(a+b+c)/(2)`
`rArr s=(2+(7)/(2)+(5)/(2))/(2)=4`
`:. (2 sinP-sin2P)/(2sin P+sin2P)=(2sinP(1-cosP))/(2sinP(1+cosP))`
`=(2sin^(2)(P//2))/(2cos^(2)(P//2))=tan^(2)(P//2)`

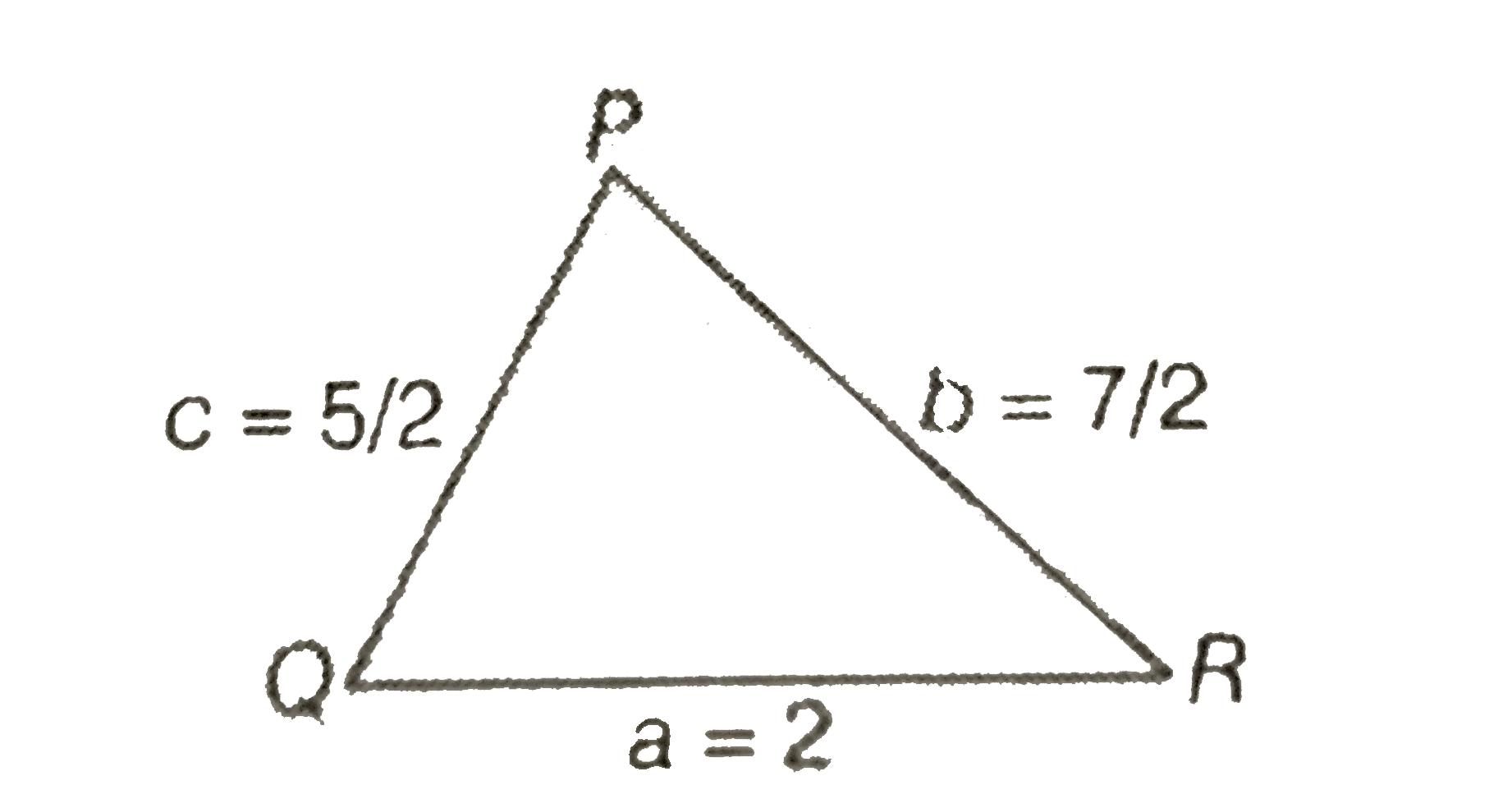
`((s-b)(s-c))/(s(s-a))xx((s-b)(s-c))/((s-b)(s-c))`
`=([(s-b)^(2)(s-c)^(2)])/(Delta^(2))((4-(7)/(2))^(2)(4-(5)/(2))^(2))/(Delta^(2))=((3)/(4Delta))^(2)`