Question

In triangle $ABC,$
let $\angle c=\frac{\pi }{2}\stackrel{.}{}$
If $r$
is the inradius and $R$
is circumradius of the triangle, then $2(r+R)$
is equal to
$a+b$

(b) $b+c$

$c+a$
(d) $a+b+c$

Options

A. a+b
B. b+c
C. c+a
D. a+b+c

Answer

A

Explanation

Here, `R^(2)=MC^(2)=1/4(a^(2)+b^(2)) " "["by distance from origin"]`
`=1/4c^(2)" "["by Pythagoras theorem"]`

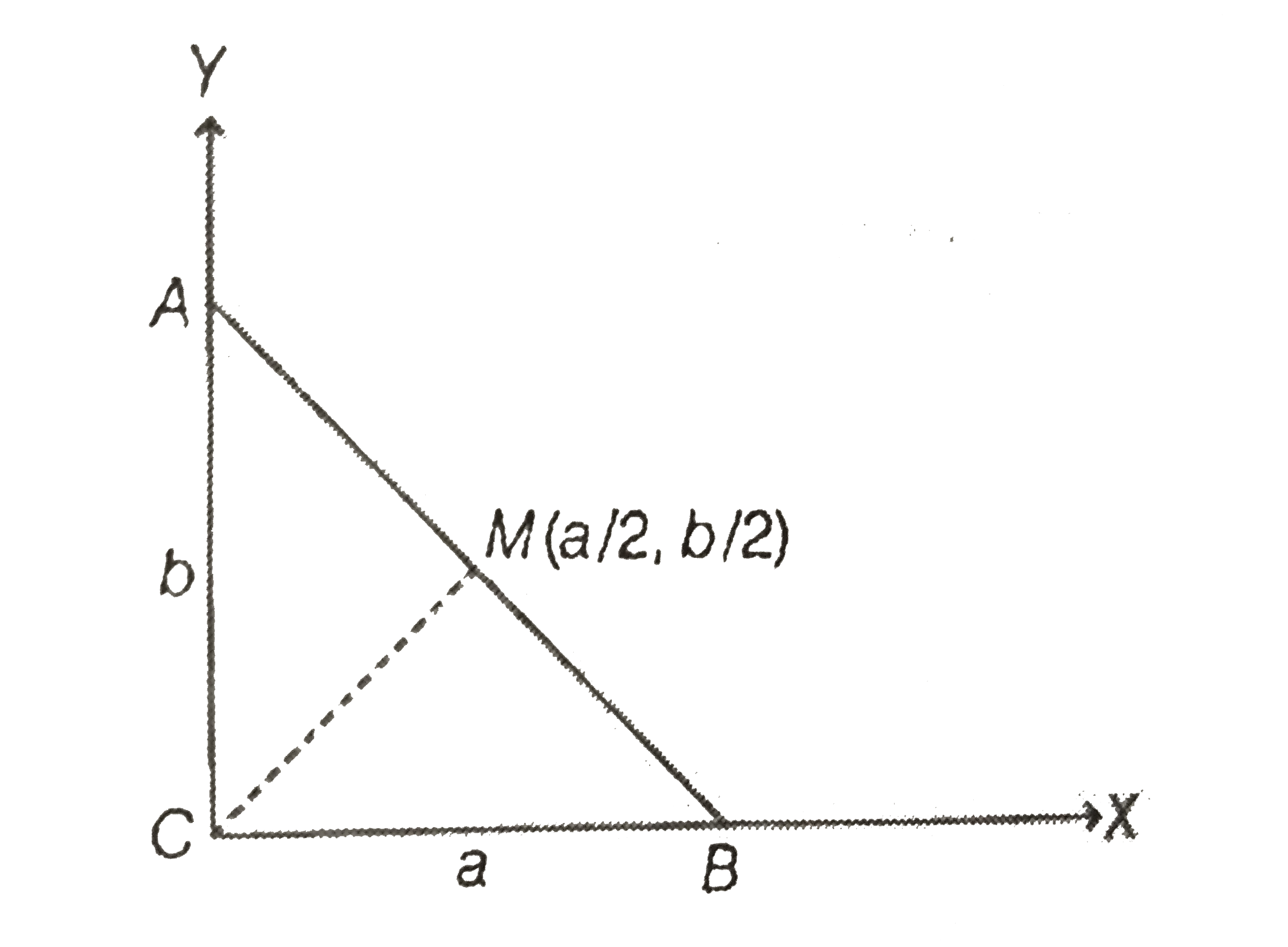
`rArr" "R=c/2`
Next, `r=(s-c)tan(C//2)=(s-c)tanpi//4=s-c`
`:." "2(r+R)=2r+2R=2s-2c+c`
=a+b+c-c
= a + b