The slope of the tangent to a curve y=f(x) at (x,f(x)) is 2x+1. If the curve passes through the point (1,2) then the area of the region bounded by the curve, the x-axis and the line x=1 is (A) 56 (B) 65 (C) 16 (D) 1
A
32
B
43
C
56
D
112
Video Solution
Text Solution
The correct Answer is:C
Given, dydx=2x+1
On integrating both sides
∫dy=∫(2x+1)dx
⇒y=x2+x+C which passes passes through(1,2)
∴2=1+1+C
⇒C=0
∴y=x2+x
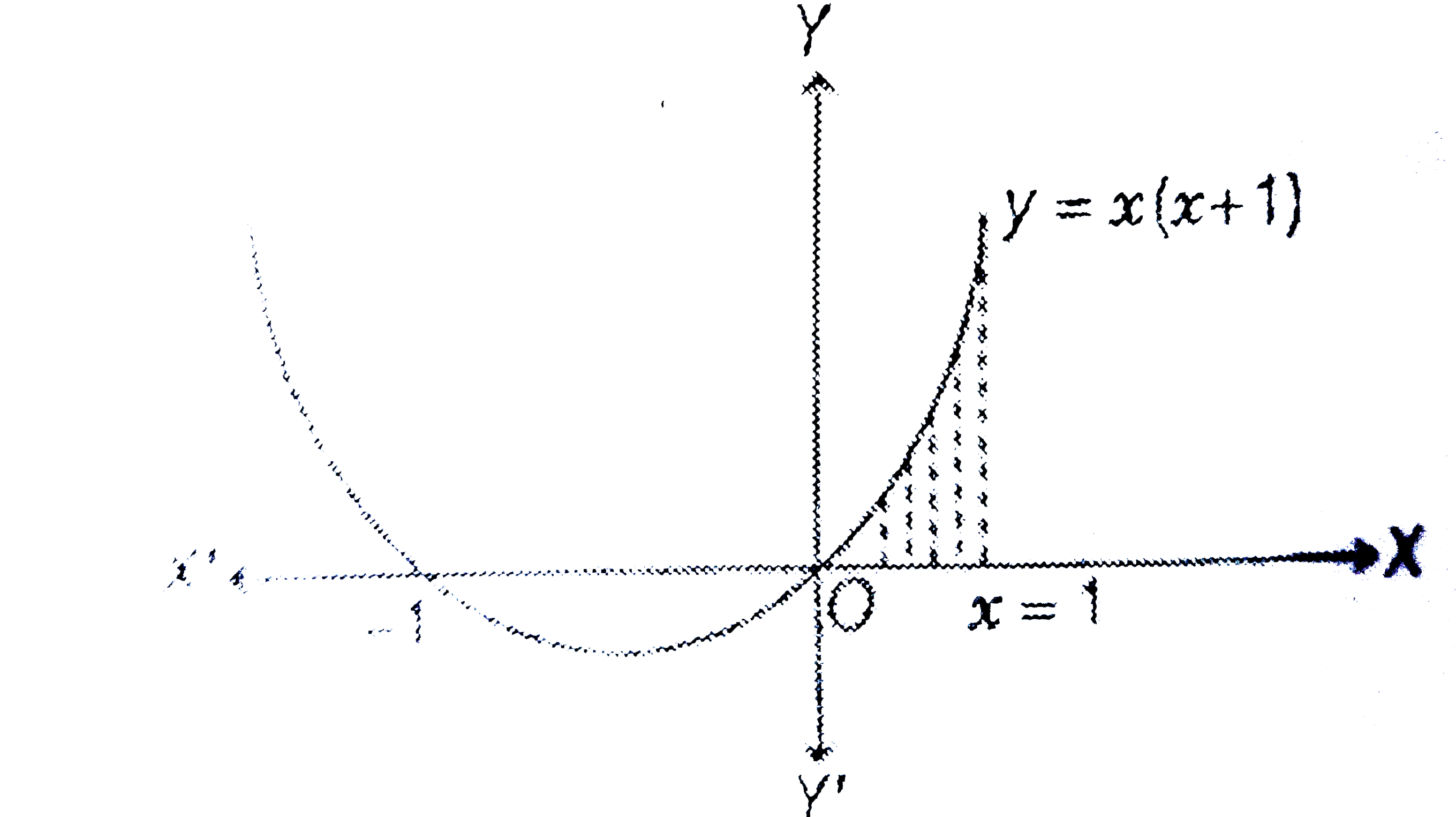
Thus, the required area bounded by X-axis, the curve and x=1
=∫10(x2+x)dx=[x33+x22]10
=13+12=56 sq unit
|
Topper's Solved these Questions
- AREABook:IIT JEE PREVIOUS YEARChapter:AREAExercise:AREA USING INTEGRATION
Explore 55 Videos
- APPLICATION OF DERIVATIVES Book:IIT JEE PREVIOUS YEARChapter:APPLICATION OF DERIVATIVES Exercise:MAXIMA AND MINIMA ( INTEGER ANSWER TYPE QUESTIONS)
Explore 8 Videos
- BINOMIAL THEOREMBook:IIT JEE PREVIOUS YEARChapter:BINOMIAL THEOREMExercise:Topic 2 Properties of Binomial Coefficent Objective Questions I (Only one correct option) (Analytical & Descriptive Questions )
Explore 8 Videos
Similar Questions
Knowledge Check
The slope of the tangent to a cruve y=f(x) at (x,f(x)0 is 2x+1.If the curve passes through the point (1,2) then the area of the region bounded by the curve,the x-axis and the lien x=1 is
A56 sq. unitsB65 sq.unitsC16 sq. unitsD6 sq. unitsThe area of the region bounded by the curve C:y=x+1x2+1 nad the line y=1 , is
Aml −12In2+π4BIn2−π4+1C12In2+π4−1DIn 2−π2+1Area bounded by the curve y=sin−1x, the X-axis and the line 2x = 1 is
Aπ12+√32Bπ12−√32Cπ12−1Dπ12+√32−1
Find the area of the region bounded by the curve (y−1)2=4(x+1) and the line y= x-1
View SolutionThe area of the region bouonded by the curve y=x−x2 between x=0 and x=1 is (A) 16 (B) 13 (C) 12 (D) 56
View SolutionFind the area of the region bounded by the curve y2=xand the lines x=1,x=4and the x-axis.
View SolutionThe area of the region bounded by the curve y=|x−2|,x=1,x=3 and the X-axis is
View SolutionThe area bounded by the curve y=x4, X-axis and the lines x = 1, x = 5 is
View Solution
