सिद्ध करें कि स्थिरवैधुत क्षेत्र के लम्बवत घटक में आवेशित पृष्ठ के एक पार्श्व (side) से दूसरे तक आसातत्य होता है जो (→E2−→E1).ˆn=σ/ε0 द्वारा व्यक्त किया जाता है जहाँ ˆn , किसी बिन्दु पर पृष्ठीय आवेश घनत्व (ˆn, कि दिशा पार्श्व 1 से पार्श्व 2 की ओर है । इस प्रकार सिद्ध करें कि चालक के ठीक बाहर वैधुत क्षेत्र σˆn/ε0 होता है।
(a) के लिए गाउस नियम का उपयोग करें और (b) के लिए इस तथ्य का कि किसी बंद लूप पर स्थिरवैधुत क्षेत्र द्वारा किया गया कार्य शून्य है ]
(a) क्योकि किसी आवेशित समतल चादर [ चित्र 6] के लिए
E=σ2ε0,
→E1=−σ2ε0ˆn और ˆE2=σ2ε0ˆn,
इसलिए (→E2−→E1)=σ2εnˆn−(−σ2ε0ˆn=σε0ˆn
स्पष्टतः →E1 और →E2, विपरीत दिशाओं में हैं , इसलिए आवेशित चादर पर असातत्य है।
क्योकि किसी चालक के अंदर वैधुत क्षेत्र नहीं होता इसलिए →E1=→0 है।
इसलिए चालक के बाहर →E=→E2=σε0ˆn

(b) ΔL लम्बाई का एक आयातकार पथ ABCD लें [ चित्र 7 ] जिसका पार्श्व AB , चालक XY के पृष्ठ I के अनुदिश है और पार्श्व CD पृष्ठ II के अनुदिश इस पथ के गिर्द यूनिट आवेश को ले जाने में किया गया कार्य
∮→E1.→dl=0

यदि पार्श्व AB और CD की अपेक्षा पार्श्व BC और AD उपेक्षणीय रूप से छोटे हो ,तो
∮→E⊙→dl=∫BA→E.→dl+∫DC→E⊙→dl
या E1tΔL−E2tΔL=0 या (E1t−E2t)ΔL=0
(E2t के साथ ऋणात्मक चिन्ह इसलिए है क्योकि AB और CD विपरीत दिशाओं में है ) E1t=E2t E1t और E2t, चालक के दोनों पार्श्वों पर वैधुत तीव्रता के स्पर्शरेखीय घटक दर्शाने हैं। इस प्रकार स्थिरवैधुत क्षेत्र का स्पर्शरेखीय घटक , आवेशित पृष्ठ के एक पार्श्व से दूसरे पार्श्व तक सतत है।
Topper's Solved these Questions
- धारिता और परावैधुत पदार्थ BOOK - GRB PUBLICATION HINDICHAPTER - धारिता और परावैधुत पदार्थ EXERCISE - प्रतियोगिता समाग्री (बहुविकल्पीय प्रश्न : एक सही विकल्प)
138 Videos
- धारिता और परावैधुत पदार्थ BOOK - GRB PUBLICATION HINDICHAPTER - धारिता और परावैधुत पदार्थ EXERCISE - प्रतियोगिता समाग्री (बहुविकल्पीय प्रश्न : एक या एक से अधिक सही विकल्प
35 Videos
- धारिता और परावैधुत पदार्थ BOOK - GRB PUBLICATION HINDICHAPTER - धारिता और परावैधुत पदार्थ EXERCISE - प्रतिरुपी अभ्यास
21 Videos
- धारा के चुम्बकीय प्रभावBOOK - GRB PUBLICATION HINDICHAPTER - धारा के चुम्बकीय प्रभावEXERCISE - NCERT पाठ्यपुस्तक अभ्यासः उत्तरों सहित
14 Videos
- नाभिक BOOK - GRB PUBLICATION HINDICHAPTER - नाभिक EXERCISE - प्रतियोगिता सामग्री (रिक्त स्थान भरना )
25 Videos
Similar Questions
चालक पेंट से कोट कि हुई एक टेबल - टेनिस की गेंद एक रेशमी धागे से लटकाई जाती है ताकि यह दो धातु की प्लेटों के बीच लटके। एक प्लेट को भूसंपर्कित किया जाता है। जबकि दूसरी एक उच्च वोल्टता जनित्र से जोड़ी जाती है। गेंद
View Solutionएक प्रोटॉन और एक इलेक्ट्रॉन , एकसमान वैधुत क्षेत्र में रखे जाते हैं।
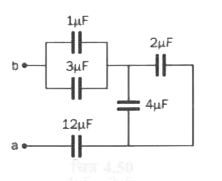
View Solutionचित्र 4.50 में दिखाए परिपथ की तुल्य धारिता ज्ञात करें।
(b ) जब a और b के बीच विभवान्तर 100 V हो , तो 12μF पर संचित हुआ आवेश निकालें।
View Solutionएक वृत्ताकार तार की कुण्डली में 100 फेरे है जिनमें से प्रत्येक का व्यासार्ध 8.0 cm है। इसमें 0.40 A धारा बढ़ती है। कुण्डली के केंद्र पर चुम्बकीय क्षेत्र B का परिमाणक्या है?
View Solutionएक परमाणु में दो इलेक्ट्रॉन , नाभिक के गिर्द R और 4R व्यासार्धों वाली वृत्ताकार कक्षाओं में घूमते हैं। और चक्कर पूरा करने के लिए उनके द्वारा लिए गए समयों का अनुपात ................ है।
View Solutionमाना कि N में एक द्वि - आधारी संकिया ∗, a∗b=a तथा b के LCM द्वारा परिभाषित है , a,b∈N तब सिद्ध कीजिए कि :(20∗16)∗8=20∗(16∗8)
View Solutionउन दो सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (0,a) से होकर जाती है तथा जिन पर बिन्दु (2a,2a) से खींचे गए लम्बो की माप a है।
View Solutionसिद्ध कीजिये कि वे बिन्दु जिनके स्थिति सदिश निम्नानुसार है , समरेख है -
2ˆi+ˆj−ˆk,3ˆi−2ˆj+ˆk,ˆi+4ˆj−3ˆk
View Solutionसिद्ध कीजिये कि वे बिन्दु जिनके स्थिति सदिश निम्नानुसार है , समरेख है -
3ˆi−2ˆj+4ˆk,ˆi+ˆj+ˆk,−ˆi+4ˆj−2ˆk
View Solutionउस सरल रेखा का सदिश समीकरण ज्ञात कीजिए जो बिन्दु 2ˆi+ˆj+3ˆk से गुजरती है तथा सदिश ˆi+2ˆj+ˆk के समान्तर है।
View Solutionसमतल का सदिश समीकरण जो बिन्दु ˆi−2ˆj+ˆk से होकर जाता है तथा सदिश 3ˆi−ˆj,2ˆk−ˆiसमान्तरहै -
View Solutionएक नली में 12 सेमी.3/से. कि दर से बालू उंडेली जा रही है। उंडेली गई बालू से एक शंकु का निर्माण इस प्रकार होता है कि शंकु कि ऊंचाई सदैव आधार कि त्रिज्या का 16 वा भाग होती ह। बालू के शंकु कि ऊंचाई में किस गति से वृद्धि हो रही है जबकि ऊंचाई 4 सेमी. है ?
View Solutionकिसी कारखाने में बने एक बल्ब कि 150 दिनों के उपयोग के बाद फ्यूज होने कि प्रायिकता 0 .05 है प्रायिकता ज्ञात कीजिए कि इस प्रकार के 5 बल्बों में से - एक से अधिक
View Solutionरेखा 4x−3y+2=0 के समांतर रेखाएं खींची गई है जो मूलबिंदु 35 से की दुरी पर है, तो निम्न में से कौन-सा एक बिंदु इनमे से किसी रेखा पर स्थित है?
View Solutionमाना √3ˆi+ˆj,ˆi+√3ˆj तथा βˆi+(1−β)ˆj क्रमश: तीन बिन्दुओ A,B तथा C के मूलबिंदु O के सापेक्ष, स्थिति सदिश है । यदि C की, OA तथा OB के बीच बने न्यूनकोण के समद्विभाजक से दुरी 3√2 है, तो β के सभी संभावित मानो का योग है
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solution
