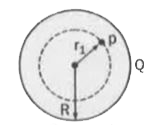
मान लें R व्यासार्ध और कुल Q आवेश वाले एक ठोस गोले का आवेश घनत्व वितरण ρ(r)=QπR4r है। गोले के केंद्र से r1 दुरी पर गोले के अंदर बिंदु P पर वैधुत क्षेत्र का परिणाम है
0
Q4πε0r21
Q2r4πε0R4
Q213πε0R4
The correct Answer is:C
P बिंदु से (r1 व्यासार्ध वाले ) गाउसीय पृष्ठ के अंदर आवेश
[ चित्र I.63 ] अर्थात
q=∫r10ρ(r)dV=∫r10[QπR4r]d(4π3r3)
=∫r10[QrπR4](4πr2dr)=Qr41R4
क्योंकि d(4π3r3)=(4π3)(3r2dr)=4πr2dr]
गाउस नियम के प्रयोग से
E(4πr21)=qε0=Qr41ε0R4
या E=Qr214πε0R4
Topper's Solved these Questions
- BOOK - GRB PUBLICATION HINDICHAPTER - धारिता और परावैधुत पदार्थ EXERCISE - प्रतियोगिता समाग्री (बहुविकल्पीय प्रश्न : एक या एक से अधिक सही विकल्प35videos
धारिता और परावैधुत पदार्थ
- BOOK - GRB PUBLICATION HINDICHAPTER - धारिता और परावैधुत पदार्थ EXERCISE - प्रतियोगिता समाग्री (बहुविकल्पीय प्रश्न : एक या एक से अधिक सही विकल्प (कॉलम मिलाना)4videos
धारिता और परावैधुत पदार्थ
- BOOK - GRB PUBLICATION HINDICHAPTER - धारिता और परावैधुत पदार्थ EXERCISE - NCERT पाठ्यपुस्तक अभ्यास : उत्तरों सहित33videos
धारिता और परावैधुत पदार्थ
- BOOK - GRB PUBLICATION HINDICHAPTER - धारा के चुम्बकीय प्रभावEXERCISE - NCERT पाठ्यपुस्तक अभ्यासः उत्तरों सहित14videos
धारा के चुम्बकीय प्रभाव
- BOOK - GRB PUBLICATION HINDICHAPTER - नाभिक EXERCISE - प्रतियोगिता सामग्री (रिक्त स्थान भरना )25videos
नाभिक
Similar Questions
एक प्रोटॉन और एक इलेक्ट्रॉन , एकसमान वैधुत क्षेत्र में रखे जाते हैं।
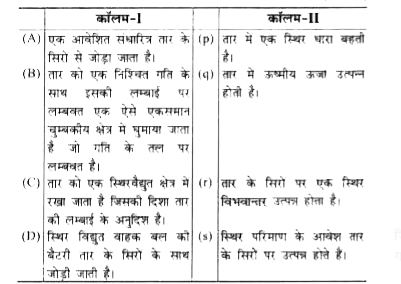
02:31View Solutionकॉलम - I में कुछ स्थितियाँ दी गई हैं जिनमें R प्रतिरोध का एक सीधा धातु का तार प्रयुक्त होता है और कॉलम - II में कुछ परिणामी प्रभाव दिए गए हैं। कॉलम - I की प्रविष्टियों को कॉलम - II की प्रविष्टियों से मिलाएँ।
 04:28View Solution
04:28View Solutionदो आवेश 5×10−8C और −3×10−8C एक दूसरे से 16cm दूर हैं इन दोनों आवेशों को जोड़ने वाली रेखा पर किस -किस बिन्दु पर वैधुत विभव शून्य है ? अनन्त पर विभव शून्य लें।
04:06View Solutionएक वृत्ताकार तार की कुण्डली में 100 फेरे है जिनमें से प्रत्येक का व्यासार्ध 8.0 cm है। इसमें 0.40 A धारा बढ़ती है। कुण्डली के केंद्र पर चुम्बकीय क्षेत्र B का परिमाणक्या है?
03:12View Solutionएक परमाणु में दो इलेक्ट्रॉन , नाभिक के गिर्द R और 4R व्यासार्धों वाली वृत्ताकार कक्षाओं में घूमते हैं। और चक्कर पूरा करने के लिए उनके द्वारा लिए गए समयों का अनुपात ................ है।
04:06View Solution−3Q तथा +2Q परिमाण के दो आवेश क्रमश (a ,0 ) और (4a ,0 ) पर रखे है। 5a त्रिज्या वाले एक गोले, जिसका केंद्र मूलबिंदु पर है , से गुजरने वाला वैधुत फ्लक्स क्या होगा ?
03:12View Solutionदो विधुतरूधर ताँबे के समरूप आवेशित गोलों A और B में क्रमश: qA और qB आवेश है। उसी साइज का तीसरा अनावेशित गोला C पहले गोले A के संपर्क में रखा जाता है। तथा उसके बाद गोले B के संपर्क में रखा जाता है। अंत में दोनों से दूर कर दिया जाता है। A और B में नए आवेश क्या होंगे ?
52:37View Solutionयदि गोले का सदिश समीकरण, →r2−→r.(8ˆi−6ˆj+10ˆk)−50=0 है, तो गोले के केन्द्र के निर्देशांक और त्रिज्या ज्ञात कीजिए।
38:22View Solutionयदि गोले का सदिश समीकरण, →r2−→r.(8ˆi−6ˆj+10ˆk)−50=0 है, तो गोले के केन्द्र के निर्देशांक और त्रिज्या ज्ञात कीजिए।
52:40View Solutionयदि गोले का सदिश समीकरण, →r2−→r.(8ˆi−6ˆj+10ˆk)−50=0 है, तो गोले के केन्द्र के निर्देशांक और त्रिज्या ज्ञात कीजिए।
45:42View Solutionयदि गोले का संदिश समीकरण r^(2) - vec( r ) . ( 8vec( i ) - 6 vec( j ) + 10 vec( k )) - 50 = 0 है तो गोले का केंद्र और त्रिज्या ज्ञात कीजिए।
35:43View Solutionकुचालक गोले के कारण वैधुत विभव
01:23:57View Solutionवृत्ताकार पथ पर आवेश की गति के कारण केंद्र पर चुंबकीय क्षेत्र|धारावाहि चाप के कारण केंद्र पर चुंबकीय क्षेत्र
45:46View Solutionआवेश के विशिष्ट गुण|आवेश एक अदिश राशि है|आवेश सदैव द्रव्यमान के साथ सम्बन्ध होता है|महतवपूर्ण बिंदु|आवेश का स्थानांतरण|आवेश का क्वांटिकरण|आवेश संरक्षित है|OMR|Summary
01:07:37View Solutionपृष्ठीय क्षेत्रफल और आयतन#!#गोले का पृष्ठीय क्षेत्रफल#!#गोले का आयतन#!#परीक्षा के लिए महत्वपूर्ण प्रश्न
40:59View Solutionपृष्ठीय क्षेत्रफल और आयतन#!#गोले के पृष्ठीय क्षेत्रफल#!#गोले का आयतन
View Solution

