If D =∣∣ ∣ ∣∣11111+x1111+y∣∣ ∣ ∣∣for x≠0,y≠0 then D is
divisible by x but not y
divisible by y but not x
divisible by neither x nor y
divisible by both x and y
The correct Answer is:D
Step by step video, text & image solution for If D =|{:(1,1,1),(1,1+x,1),(1,1,1+y):}|"for" " "xne0,yne0 then D is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DETERMINANTSBOOK - DISHA PUBLICATIONCHAPTER - DETERMINANTSEXERCISE - EXERCISE -2 CONCEPT APPLICATOR
30 Videos
- DETERMINANTSBOOK - DISHA PUBLICATIONCHAPTER - DETERMINANTSEXERCISE - EXERCISE -2 CONCEPT APPLICATOR
30 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - DISHA PUBLICATIONCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise-2 : Concept Applicator
30 Videos
- DIFFERENTIAL EQUATIONS BOOK - DISHA PUBLICATIONCHAPTER - DIFFERENTIAL EQUATIONS EXERCISE - Exercise-2 : Concept Applicator
30 Videos
Similar Questions
If D=|11111+x1111+y|f o rx≠0,y≠0 then D is (1) divisible by neither x nor y (2) divisible by both x and y (3) divisible by x but not y (4) divisible by y but not x
View SolutionLet A=⎡⎢⎣12101−1311⎤⎥⎦. Find the sum of all the value of λ for which there exists a column vertor X≠0 such that AX=λX.
View Solution
Knowledge Check
If D =∣∣ ∣ ∣∣11111+x1111+y∣∣ ∣ ∣∣for x≠0,y≠0 then D is
Adivisible by neither x nor yBdivisible by both x and yCdivisible by x but not yDdivisible by y but not xIf D=∣∣ ∣ ∣∣11111+x1111+y∣∣ ∣ ∣∣ for x≠0,y≠0, then D is divisible by
Ax but not yBy but not xCneither x nor yDboth x and yIf f(x)={1−cosxxx≠0kx=0 is continuous at x=0, then the value of k is
A0B12C14D−12
If a,b,c and d are the roots of the equation
x4+2x3+4x2+8x+16=0 the value of the determinant ∣∣ ∣ ∣ ∣∣1+a11111+b11111+c11111+d∣∣ ∣ ∣ ∣∣ is
View SolutionThe truth table for the following combination of gates is
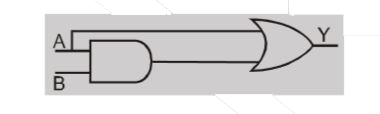
(a) ABY000010101111
(b) ABY000010100111
(c) ABY001011101110
(d) ABY0000111011110
View Solution24. Eigen values of⎡⎢⎣111111111⎤⎥⎦ are (a) 0,00 (b) 0, 01 (c) 0, 0, 3 (d)1, 1, 1
View SolutionIf f(x)={[x]−1x−1,x≠10 ,x=1 then f(x) is
View SolutionIf : f(x2+1x)=x4+1x2, where x≠0, then: f'(3)=
View Solution
