The numerical value of Young's modulus in S.I. unit is β. what is its numerical value in CGS system?
β
10β
β/10
100β
The correct Answer is:B
To find the numerical value of Young's modulus in the CGS system when its value in the SI system is given as β, we can follow these steps:
1. Understanding Young's Modulus:
Young's modulus (Y) is defined as the ratio of stress to strain. The formula for Young's modulus is:
\(
Y = \frac{\text{Stress}}{\text{Strain}}
\)
Stress is defined as force per unit area.
2. Units in SI System:
In the SI system, the unit of force is Newton (N) and the unit of area is square meters (m²). Therefore, the unit of Young's modulus in SI is:
\(
\text{SI unit of } Y = \frac{\text{N}}{\text{m}^2}
\)
3. Convert SI Units to CGS Units:
We need to convert the units from SI to CGS. In the CGS system:
- 1 Newton (N) = \(10^5\) Dynes (dyn)
- 1 meter (m) = \(10^2\) centimeters (cm)
4. Substituting the Units:
Now, substituting these conversions into the formula for Young's modulus:
\(
Y = \frac{10^5 \text{ dyn}}{(10^2 \text{ cm})^2}
\)
Simplifying the denominator:
\(
(10^2 \text{ cm})^2 = 10^4 \text{ cm}^2
\)
Thus, we have:
\(
Y = \frac{10^5 \text{ dyn}}{10^4 \text{ cm}^2}
\)
5. Calculating the Numerical Value:
Simplifying the expression:
\(
Y = 10^{5-4} \text{ dyn/cm}^2 = 10^{1} \text{ dyn/cm}^2 = 10 \text{ dyn/cm}^2
\)
6. Relating to Beta:
Since we know that the numerical value of Young's modulus in SI units is β, we can express the value in the CGS system as:
\(
\text{Numerical value in CGS} = 10 \beta
\)
Final Answer:
The numerical value of Young's modulus in the CGS system is \(10 \beta\).
Young's modulus (Y) is defined as the ratio of stress to strain. The formula for Young's modulus is:
\(
Y = \frac{\text{Stress}}{\text{Strain}}
\)
Stress is defined as force per unit area.
In the SI system, the unit of force is Newton (N) and the unit of area is square meters (m²). Therefore, the unit of Young's modulus in SI is:
\(
\text{SI unit of } Y = \frac{\text{N}}{\text{m}^2}
\)
We need to convert the units from SI to CGS. In the CGS system:
- 1 Newton (N) = \(10^5\) Dynes (dyn)
- 1 meter (m) = \(10^2\) centimeters (cm)
Now, substituting these conversions into the formula for Young's modulus:
\(
Y = \frac{10^5 \text{ dyn}}{(10^2 \text{ cm})^2}
\)
Simplifying the denominator:
\(
(10^2 \text{ cm})^2 = 10^4 \text{ cm}^2
\)
Thus, we have:
\(
Y = \frac{10^5 \text{ dyn}}{10^4 \text{ cm}^2}
\)
Simplifying the expression:
\(
Y = 10^{5-4} \text{ dyn/cm}^2 = 10^{1} \text{ dyn/cm}^2 = 10 \text{ dyn/cm}^2
\)
Since we know that the numerical value of Young's modulus in SI units is β, we can express the value in the CGS system as:
\(
\text{Numerical value in CGS} = 10 \beta
\)
The numerical value of Young's modulus in the CGS system is \(10 \beta\).
Topper's Solved these Questions
- PHYSICAL WORLD, UNITS AND MEASUREMENTSBOOK - DISHA PUBLICATIONCHAPTER - PHYSICAL WORLD, UNITS AND MEASUREMENTSEXERCISE - Exercise - 1 : Concept Builder (Topicwise)(Topic 2 : Errors in Measurements and Significant Figures)
28 Videos
- PHYSICAL WORLD, UNITS AND MEASUREMENTSBOOK - DISHA PUBLICATIONCHAPTER - PHYSICAL WORLD, UNITS AND MEASUREMENTSEXERCISE - Exercise - 1 : Concept Builder (Topicwise)(Topic 3 : Dimensions of Physical Quantities)
22 Videos
- PHYSICAL WORLD, UNITS AND MEASUREMENTSBOOK - DISHA PUBLICATIONCHAPTER - PHYSICAL WORLD, UNITS AND MEASUREMENTSEXERCISE - Exercise - 2 : Concept Applicator
30 Videos
- OSCILLATIONS BOOK - DISHA PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Exercise-2 : Concept Applicator
28 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - DISHA PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Exercise -2 : Concept Applicator
26 Videos
Similar Questions
Knowledge Check
The unit of Young’s modulus is
ANm2BNm−2CNmDNm−1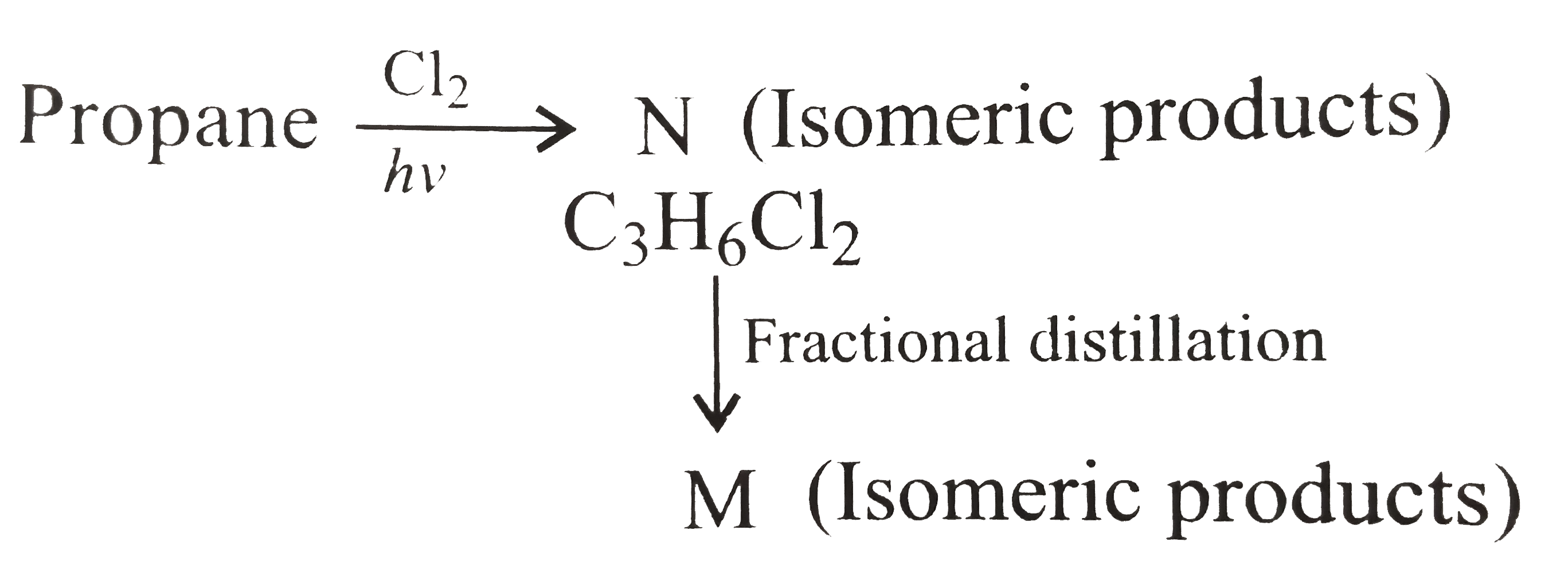
What are the numerical values of N and M?A6,6B5,4C4,4D3,3Numerical value of Faraday's constant is :
A96500 CB96800 CC95600 CD96400 C
Write the numerical value of h and its unit
View SolutionIf the numerical value of power of this lens is 10 D, what is the focal length in the Cartesian system?
View SolutionWhat is the value of the gas constant in S.I. units ?
View SolutionIn MKS system, unit of Young's modulus is
View SolutionThe numerical value of density in SI is n times its value in cgs system. The value of n is
View Solution
