from the following combinations of physical constants (expressed through their as usual symbols) the only combination, that would have the same value in different systems of units, is:
ch2πε2o
e22πεoGm2e
μoεoc2Ghe2
(2π√μoεoce2hG
The correct Answer is:B
To solve the problem of identifying which combination of physical constants has the same value in different systems of units, we need to analyze each option for dimensional consistency. The only combination that will yield a dimensionless quantity will have the same value regardless of the unit system used.
Let's evaluate the options step by step:
Step 1: Analyze Option A
Combination: ch2πϵ20
- Constants:
- c (speed of light): dimensions (LT−1)
- h (Planck's constant): dimensions (ML2T−1)
- ϵ0 (permittivity of free space): dimensions (M−1L−3T4A2)
Calculating Dimensions:
Dimensions of ϵ20=(M−1L−3T4A2)2=M−2L−6T8A4
Now substituting into the expression:
ch2πϵ20=(LT−1)(ML2T−1)M−2L−6T8A4
Calculating the dimensions:
=ML3T−2M−2L−6T8A4=M3L9T−10A−4
This is not dimensionless.
Conclusion: Option A is not dimensionless.
Step 2: Analyze Option B
Combination: e22πϵ0gm2e
- Constants:
- e (charge): dimensions (M1/2L3/2T−1)
- g (gravitational constant): dimensions (M−1L3T−2)
- me (mass of electron): dimensions (M)
Calculating Dimensions:
e2=(M1/2L3/2T−1)2=ML3T−2
Now substituting into the expression:
e22πϵ0gm2e=ML3T−2M−1L3T−2⋅M2
Calculating the dimensions:
=ML3T−2M1L3T−2=M0L0T0=1
This is dimensionless.
Conclusion: Option B is dimensionless.
Step 3: Analyze Option C
Combination: μ0ϵ0ghc2e2
- Constants:
- μ0 (permeability of free space): dimensions (MLT−2A−2)
- ϵ0: dimensions (M−1L−3T4A2)
- g: dimensions (M−1L3T−2)
- h: dimensions (ML2T−1)
- c: dimensions (LT−1)
Calculating Dimensions:
The combined dimensions will be complex and will not simplify to a dimensionless quantity upon calculation.
Conclusion: Option C is not dimensionless.
Step 4: Analyze Option D
Combination: √μ0ϵ0g
- Constants: Same as above.
Calculating Dimensions:
This will also yield a complex dimensional analysis that does not simplify to a dimensionless quantity.
Conclusion: Option D is not dimensionless.
Final Answer:
The only combination that is dimensionless is Option B: e22πϵ0gm2e.
Combination: ch2πϵ20
- c (speed of light): dimensions (LT−1)
- h (Planck's constant): dimensions (ML2T−1)
- ϵ0 (permittivity of free space): dimensions (M−1L−3T4A2)
Dimensions of ϵ20=(M−1L−3T4A2)2=M−2L−6T8A4
Now substituting into the expression:
ch2πϵ20=(LT−1)(ML2T−1)M−2L−6T8A4
Calculating the dimensions:
=ML3T−2M−2L−6T8A4=M3L9T−10A−4
This is not dimensionless.
Combination: e22πϵ0gm2e
- e (charge): dimensions (M1/2L3/2T−1)
- g (gravitational constant): dimensions (M−1L3T−2)
- me (mass of electron): dimensions (M)
e2=(M1/2L3/2T−1)2=ML3T−2
Now substituting into the expression:
e22πϵ0gm2e=ML3T−2M−1L3T−2⋅M2
Calculating the dimensions:
=ML3T−2M1L3T−2=M0L0T0=1
This is dimensionless.
Combination: μ0ϵ0ghc2e2
- μ0 (permeability of free space): dimensions (MLT−2A−2)
- ϵ0: dimensions (M−1L−3T4A2)
- g: dimensions (M−1L3T−2)
- h: dimensions (ML2T−1)
- c: dimensions (LT−1)
The combined dimensions will be complex and will not simplify to a dimensionless quantity upon calculation.
Combination: √μ0ϵ0g
This will also yield a complex dimensional analysis that does not simplify to a dimensionless quantity.
The only combination that is dimensionless is Option B: e22πϵ0gm2e.
Topper's Solved these Questions
- BOOK - DISHA PUBLICATIONCHAPTER - PHYSICAL WORLD, UNITS AND MEASUREMENTSEXERCISE - Exercise - 1 : Concept Builder (Topicwise)(Topic 3 : Dimensions of Physical Quantities)22videos
PHYSICAL WORLD, UNITS AND MEASUREMENTS
- BOOK - DISHA PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Exercise-2 : Concept Applicator28videos
OSCILLATIONS
- BOOK - DISHA PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Exercise -2 : Concept Applicator26videos
RAY OPTICS AND OPTICAL INSTRUMENTS
Similar Questions
Knowledge Check
- Question 1 - Select One
From the following combinations of physical constants (expressed through their usual symbols) the only combination that would have the same value in different systems of units is :
Ach2πɛ20Be22πɛ0Gm2eCm0ɛ0c2Ghe2D2π√μ0ɛ0ce2hG - Question 2 - Select One
The correct combination is (symbols have their usual meanings)
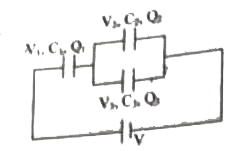 AQ1=Q2=Q3andV1=V2=V3=VBQ1=Q2+Q3andV=V1+V2+V3CQ1=Q2+Q3andV=V1+V2DQ2=Q3andV2=V3
AQ1=Q2=Q3andV1=V2=V3=VBQ1=Q2+Q3andV=V1+V2+V3CQ1=Q2+Q3andV=V1+V2DQ2=Q3andV2=V3 - Question 3 - Select One
The physical quantity having the same unit in all the systems of unit is ________ .
AlengthBtimeCmassDfoot
Which of the following physical quantities has same unit in all the three system of units?
View SolutionOne of the combination from the fundamental physical constants is hc/G. The unit of this expression is
View SolutionWhich of the following shows the correct expression of height d time to catch a ball dropped from the top of a tower ? (symbols have their usual meaning)
View SolutionThe value of which one of the following quantity remains same in all system of units ?
View SolutionThe value of which one of the following quantities remains same in all systems of units?
View Solution