A ball dropped from a point A falls down vertically to C, through the midpoint B. The descending time from A to B and that from A to C are in the ratio
1:1
1:2
1:3
1:√2
The correct Answer is:D
To find the ratio of descending times from point A to point B and from point A to point C, we can follow these steps:
Step 1: Define the distances
Let the distance from point A to point B be x. Since B is the midpoint of AC, the distance from point B to point C is also x. Therefore, the total distance from A to C is:
AC=AB+BC=x+x=2x
Step 2: Calculate time from A to B (t1)
Using the equation of motion:
s=ut+12at2
For the motion from A to B:
- Initial velocity u=0 (the ball is dropped)
- Displacement s=x
- Acceleration a=g (acceleration due to gravity)
Substituting these values into the equation:
x=0⋅t1+12gt21
This simplifies to:
x=12gt21
Rearranging gives:
t21=2xg
Taking the square root:
t1=√2xg
Step 3: Calculate time from A to C (t2)
Using the same equation of motion for the motion from A to C:
- Displacement s=2x
Substituting into the equation:
2x=0⋅t2+12gt22
This simplifies to:
2x=12gt22
Rearranging gives:
t22=4xg
Taking the square root:
t2=√4xg=2√xg
Step 4: Find the ratio of times t1t2
Now we can find the ratio of t1 to t2:
t1t2=√2xg2√xg
This simplifies to:
t1t2=√22=1√2
Final Answer
The ratio of the descending time from A to B and from A to C is:
t1t2=1√2
Let the distance from point A to point B be x. Since B is the midpoint of AC, the distance from point B to point C is also x. Therefore, the total distance from A to C is:
AC=AB+BC=x+x=2x
Using the equation of motion:
s=ut+12at2
For the motion from A to B:
- Initial velocity u=0 (the ball is dropped)
- Displacement s=x
- Acceleration a=g (acceleration due to gravity)
x=0⋅t1+12gt21
This simplifies to:
x=12gt21
Rearranging gives:
t21=2xg
Taking the square root:
t1=√2xg
Using the same equation of motion for the motion from A to C:
- Displacement s=2x
2x=0⋅t2+12gt22
This simplifies to:
2x=12gt22
Rearranging gives:
t22=4xg
Taking the square root:
t2=√4xg=2√xg
Now we can find the ratio of t1 to t2:
t1t2=√2xg2√xg
This simplifies to:
t1t2=√22=1√2
The ratio of the descending time from A to B and from A to C is:
t1t2=1√2
Topper's Solved these Questions
- BOOK - DISHA PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Exercise-230videos
MOTION IN A STRAIGHT LINE
- BOOK - DISHA PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Exercise-230videos
MOTION IN A STRAIGHT LINE
- BOOK - DISHA PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Exercise -2 : CONCEPT APPLICATOR28videos
MOTION IN A PLANE
- BOOK - DISHA PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - EXERCISE - 2 : Concept Applicator25videos
MOVING CHARGES AND MAGNETISM
Similar Questions
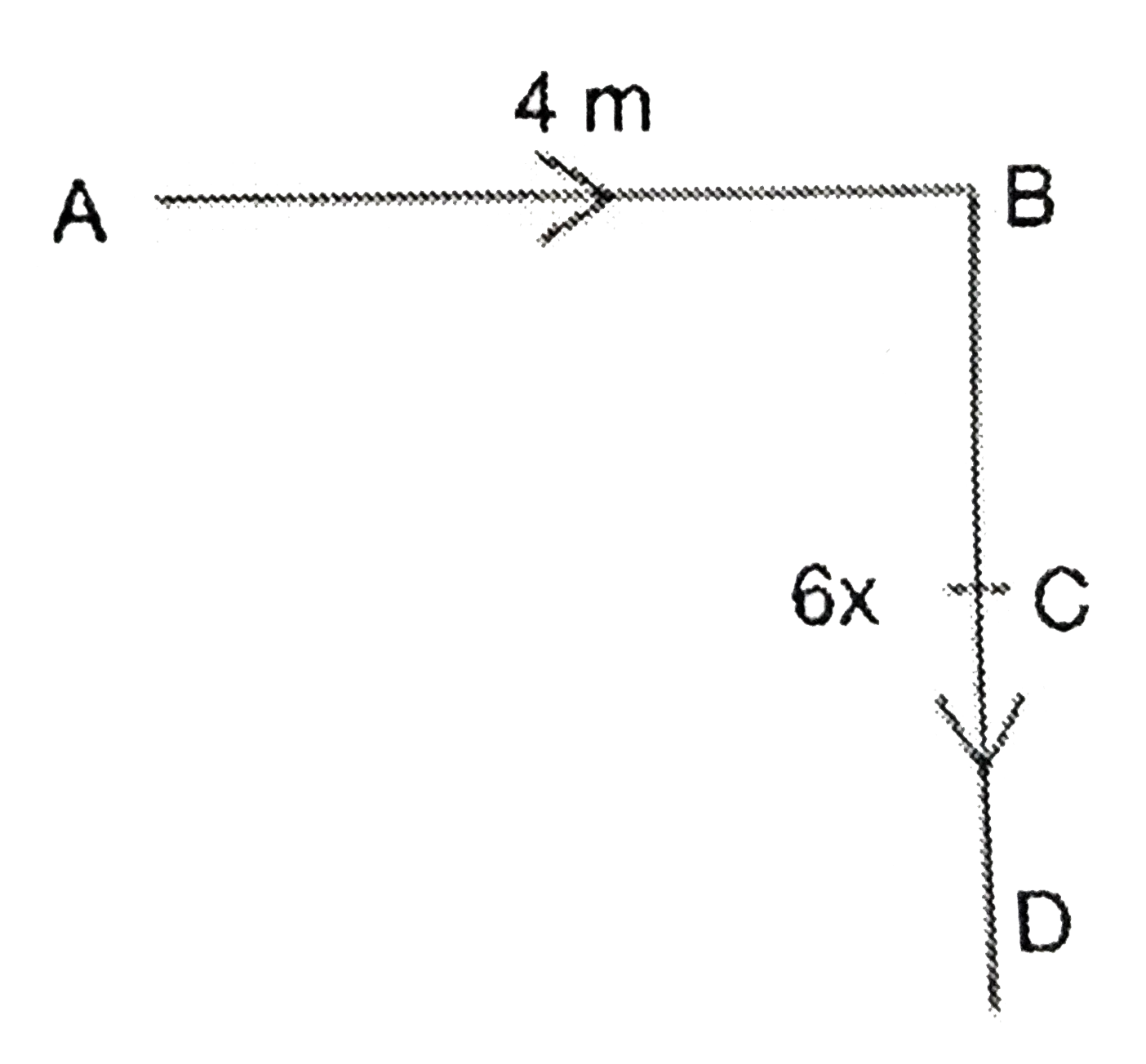
A person starsts from point A and reaches point C which is the midpoint of BD. If the takes four seoconds time, then determine
(a) the average speed
(b) the average velocity
 View Solution
View SolutionA point moving with constant acceleration from A to B in the straight line AB has velocities u and v at and B respectively. Find its velocity at C, the mid point of AB. Also show that if the time from A to C is twice that from C to B, then v=7u.
View Solution
Knowledge Check
- Question 1 - Select One
A ball is dropped from a height of 10 m, as it falls,
Aits velocity increases and acceleration decreases.Bits velocity decreases and acceleration increases.Cits velocity increases and acceleration remains constant.Dits velocity and acceleration remains constant. - Question 2 - Select One
In any !ABC ,the distance of the orthocentre from the vertices A, B,C are in the ratio
Asin A : sin B : sin CBcos A : cos B : cos CCtan A : tan B: tan CDnone of these - Question 3 - Select One
A particle is dropped from point A at a certain height from ground. It falls freely and passes through thre points B,C and D with BC=CD. The time taken by the particle to move from B to CD is 2s and from C to D is 1s. The time taken to move from A to B is s
A0.5sB1.5sC0.75sD0.25s
Let A, B and C be points in a vertical line at height h, 4h5andh5 and from the ground. A particle released from rest from the point A reaches the ground in time T. The time taken by the particle to go from B to C is TBC . Then T(TBC)2=
View SolutionA ball P is dropped vertically and another ball Q is thrown horizontally with the same velocities from the same height and at the same time. If air resistance is neglected, then
View SolutionA ball is released from point A. During its motion ball takes two seconds from B to C Find the time taken by ball from A to C.
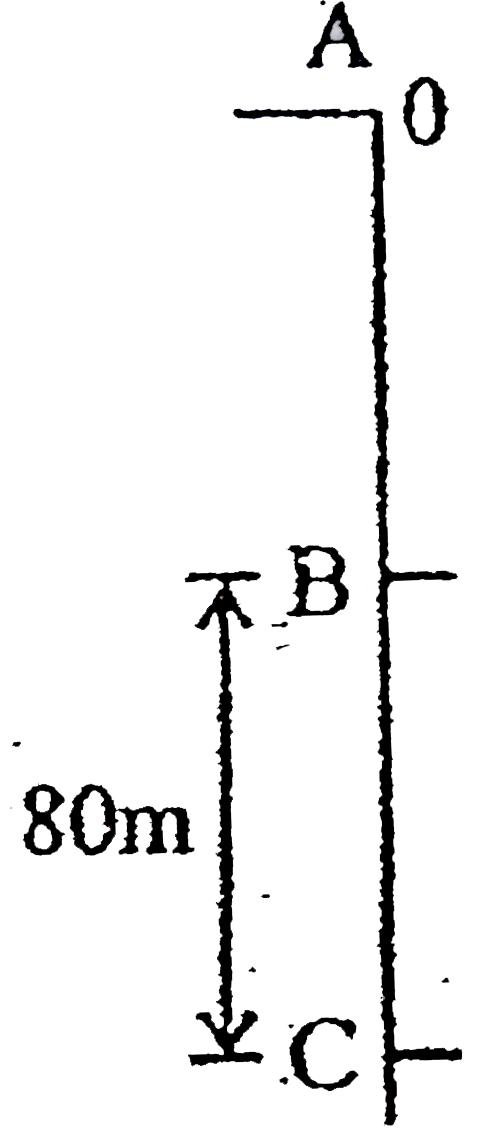 .View Solution
.View SolutionA ball is released from point A. During its motiom ball takes two seconds from B to C, Find the time taken by ball from A to C.
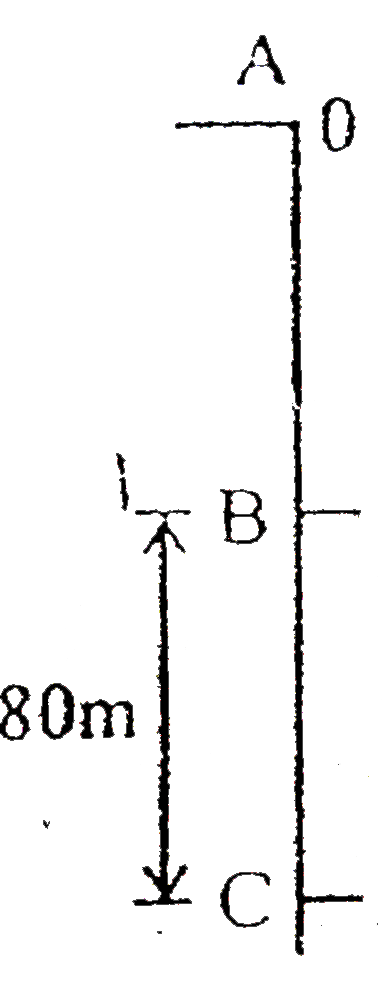 View Solution
View SolutionLet A, B, C, D be points on a vertical line such that AB = BC = CD. If a body is released from position A, the times of descent through AB, BC and CD are in the ratio.
View Solution

