A ball thrown down the incline strikes at a point on the incline 25m below the horizontal as shown in the figure. If the ball rises to a maximum height of 20 m above the point of projection, the angle of projection $α$ (with horizontal x-axis) is

${tan}^{- 1} \frac{4}{3}$

${tan}^{- 1} \frac{3}{4}$

${tan}^{- 1} \frac{3}{2}$

${tan}^{- 1} \frac{2}{3}$

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

A ball thrown by one player reaches the other in $2 s$ . The maximum height attained by the ball above the point of projection will be about.
A2.5 m
B5 m
C7.5 m
D10 m
A ball is projected horizontally from an inclined plane with a velocity V, as shown in the figure. It will strike the plane after a time

A $\frac{v_{0}}{\sqrt{3} g}$
B $\frac{2 v_{0}}{\sqrt{3} g}$
C $\frac{v_{0}}{g}$
D $\frac{2 \sqrt{3} v_{0}}{g}$
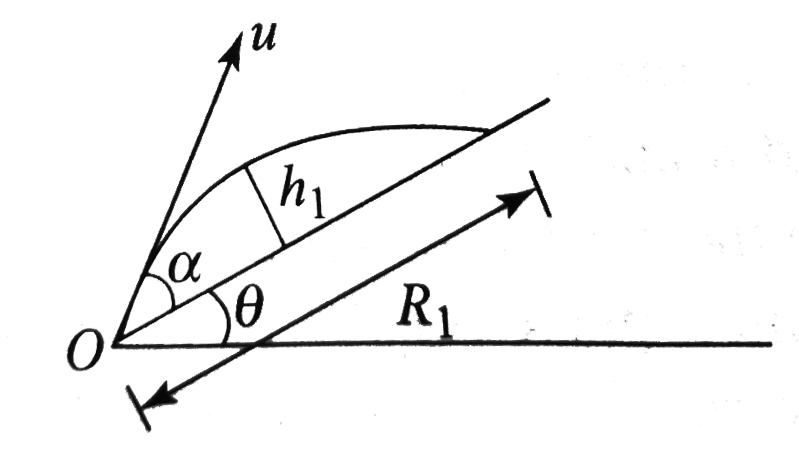
Two balls are thrown from an inclined plane at angle of projection $α$ with the plane one up the incline plane and other down the incline as shown in the figure. If $R_{1}$ & $R_{2}$ be their respective ranges, then:
A $h_{1} = h_{2}$
B $R_{2} - R_{1} = T_{1}^{2}$
C $R_{2} - R_{1} = g sin θ T_{2}^{2}$
D $R_{2} - R_{1} = g sin θ T_{1}^{2}$