The vessels A and B of equal volume and weight are immersed in water to depth h.The vessel A has an opening at the bottom through which water can enter.If the work done in immersing A and B are WA and WB respectively,then
WA=WB
WA<WB
WA>WB
None of these
The correct Answer is:B
To solve the problem, we need to analyze the work done in immersing the two vessels A and B in water to a depth h.
1. Understanding the Setup:
- Both vessels A and B have equal volume and weight.
- Vessel A has an opening at the bottom, allowing water to enter, while vessel B is closed.
2. Weight Considerations:
- When vessel A is immersed, water enters through the opening, increasing its weight.
- Vessel B remains closed, so its weight does not change when immersed.
3. Forces Acting on the Vessels:
- The weight of vessel A increases as it fills with water, while the weight of vessel B remains constant.
- The buoyant force acting on both vessels is equal to the weight of the water displaced, which is the same for both vessels since they are of equal volume.
4. External Force Required:
- To sink vessel A, the external force FA must overcome the buoyant force and the weight of the water inside it.
- For vessel B, the external force FB must only overcome the buoyant force and its own weight.
5. Comparison of Forces:
- Since vessel A gains additional weight from the water entering it, the external force FA required to immerse it is less than the external force FB required for vessel B.
- Therefore, we have FA<FB.
6. Work Done Calculation:
- Work done is defined as the force applied multiplied by the distance moved in the direction of the force.
- For vessel A, the work done WA is given by:
WA=FA⋅h
- For vessel B, the work done WB is given by:
WB=FB⋅h
7. Conclusion:
- Since FA<FB, it follows that:
WA<WB
- Hence, the work done in immersing vessel A is less than the work done in immersing vessel B.
Final Result:
WA<WB
- Both vessels A and B have equal volume and weight.
- Vessel A has an opening at the bottom, allowing water to enter, while vessel B is closed.
- When vessel A is immersed, water enters through the opening, increasing its weight.
- Vessel B remains closed, so its weight does not change when immersed.
- The weight of vessel A increases as it fills with water, while the weight of vessel B remains constant.
- The buoyant force acting on both vessels is equal to the weight of the water displaced, which is the same for both vessels since they are of equal volume.
- To sink vessel A, the external force FA must overcome the buoyant force and the weight of the water inside it.
- For vessel B, the external force FB must only overcome the buoyant force and its own weight.
- Since vessel A gains additional weight from the water entering it, the external force FA required to immerse it is less than the external force FB required for vessel B.
- Therefore, we have FA<FB.
- Work done is defined as the force applied multiplied by the distance moved in the direction of the force.
- For vessel A, the work done WA is given by:
WA=FA⋅h
- For vessel B, the work done WB is given by:
WB=FB⋅h
- Since FA<FB, it follows that:
WA<WB
- Hence, the work done in immersing vessel A is less than the work done in immersing vessel B.
WA<WB
Topper's Solved these Questions
- CONCEPT BUILDERBOOK - DISHA PUBLICATIONCHAPTER - CONCEPT BUILDEREXERCISE - Exercise-1 Concept Builder (Topic 2:Energy)
15 Videos
- CONCEPT BUILDERBOOK - DISHA PUBLICATIONCHAPTER - CONCEPT BUILDEREXERCISE - Exercise-1 Concept Builder (topic 3:Power)
20 Videos
- CONCEPT BUILDERBOOK - DISHA PUBLICATIONCHAPTER - CONCEPT BUILDEREXERCISE - Exercise-2 Concept Applicator
27 Videos
- COMMUNICATION SYSTEM BOOK - DISHA PUBLICATIONCHAPTER - COMMUNICATION SYSTEM EXERCISE - EXERCISE-2 : Concept Applicator
30 Videos
- CURRENT ELECTRICITYBOOK - DISHA PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-2 Concept Applicator
23 Videos
Similar Questions
Two bodies of equal weight and volume and having the same shape, except that one has an opening at the bottom and the other is sealed, are immersed to the same depth in water. Is less work required to immerse one than the other? If so, which one and why?
View SolutionTwo vessels A and B are filled with water at 4∘C .Vessel A is heated and vessel B is cooled.Then water overflows in
View Solution
Knowledge Check
Consider the two process on a system as shown in figure. The volumes in the initial state and in the final state are the same in the two process A and B. If W1 and W2 be the work done by the system in the processes A and B respectively then-
 AW1>W2BW1=W2CW1<W2Dnothing canbe said about the relation between W1 and W2
AW1>W2BW1=W2CW1<W2Dnothing canbe said about the relation between W1 and W2A tube of uniform cross section is used to siphon water from a vessel V as shown in the figure. The pressure over the open end of water in the vessel is atmospheric pressure (P0). The height of the tube above and below the water level in the vessel are h1 and h2, respectively.

Determine the velocity vB of the water issuing out at B.AvB=√2gh2BvB=√2h(h1+h2)CvB=√2h(h2−h1)DvB=√gh2Two vessels A and B of different shapes have the same base area and are filled with water up to the same height h (see figure). The force exerted by water on the base is FA for vessel A and FB for vessel B. The respective weights of the water filled in vessels are WA and WB. Then
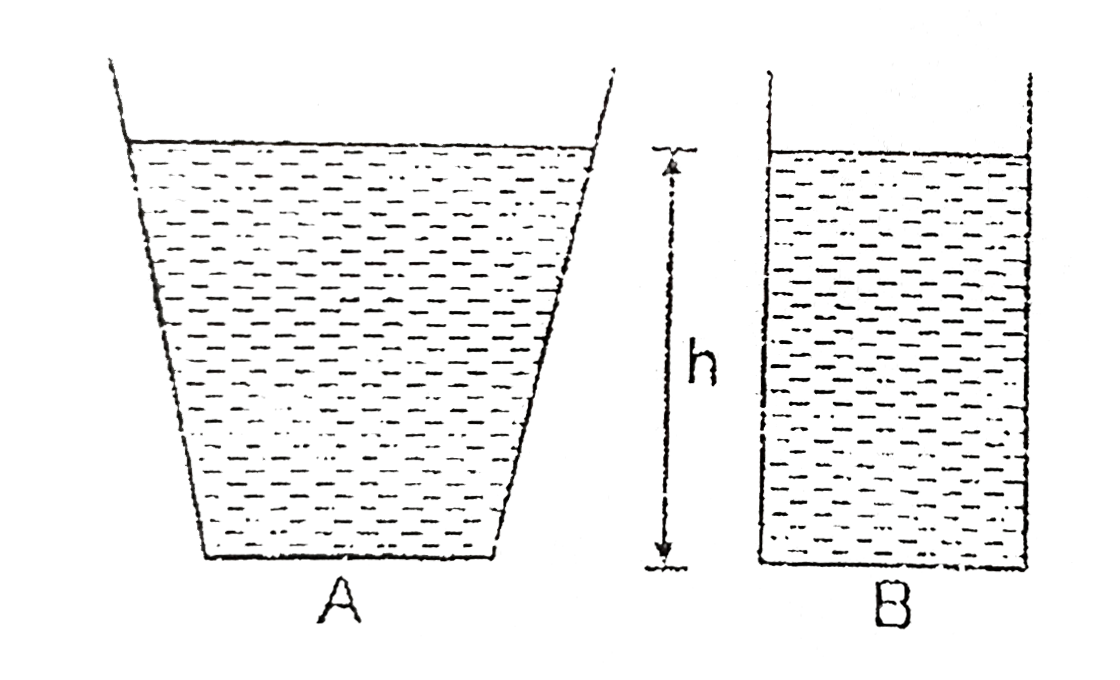 AFA>FB,WA>WBBFA=FB,WA>WBCFA=FB,WA<WBDFA>FB,WA=WB
AFA>FB,WA>WBBFA=FB,WA>WBCFA=FB,WA<WBDFA>FB,WA=WB
Two vessels A and B of equal volume (V0) are connected by a narrow tube which can be closed by a value. The vessels are fitted with piston which can be moved to change the volumes. Initially, the valve is open and the vessels contain an ideal gas (CpCv=γ) at atomspheric pressures(P0) and atmoshpeheric temperature (T0). The walls of the vessels A are diathermic and those of B are adiabatic. The value is now closed and the pistons are slowly pulled out to increase the volumes of the of the vessels to dobuled the original value.(a) Find the temperatures and pressures in the two vessels. (b) The value is now opened for sufficeint time so that the gases acquire a common tempertures and pressures . Find the new values of the temperatuere and the pressures.
View SolutionTwo vessels A and B of different shapes have the same base area and are filled with water up to the same height h (see figure). The force exerted by water on the base is FA for vessel A and FB for vessel B. The respective weights of the water filled in vessels are WA and WB. Then

View SolutionThe height of water in a vessel is h. The vessel wall of width b is at an angle θ to the vertical. The net force exerted by the water on the wall is

View SolutionThree vessels A,B,and C of different shapes contain a water upto the same height as shown in the figure .PA,PB ,and PC be the pressure exerted by the water at the bottom of the vessels A ,B and C respectively . Then
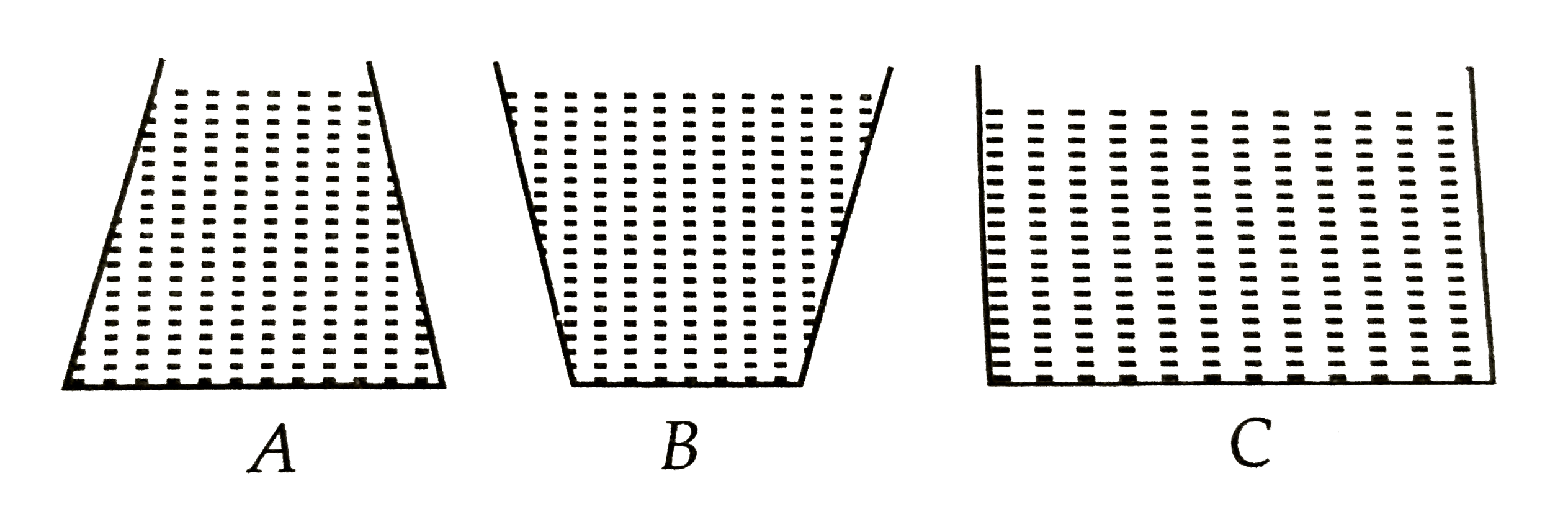
View SolutionThree vessels A, B and C of different shapes contain water upto the same height in the figure. PA,PBandPC be the pressure exerted by the water at the bottom of the vessels A, B and C respectively. Then
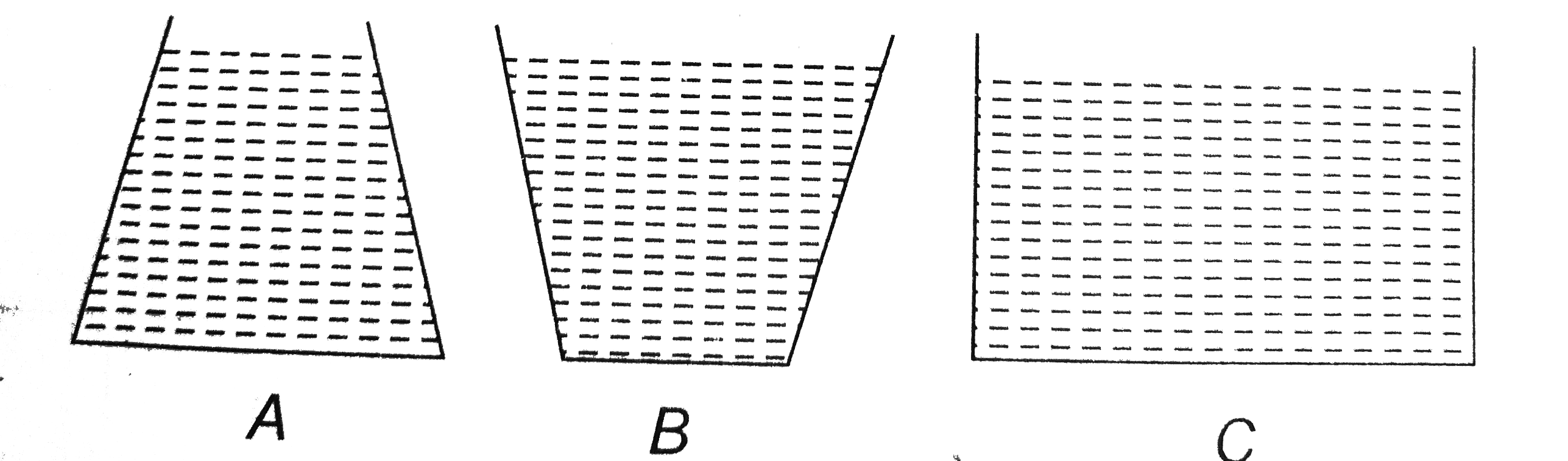
View Solution
